
Porque Entender o Agrupamento Ajuda no Ensino das Atividades de Matemática
O agrupamento é a base da Matemática. Pode-se dizer que a Matemática começou pela necessidade de se saber qual a quantidade existente em um grande grupo.
Entender o agrupamento ajuda o aluno do Ensino Fundamental I a não cometer erros nas contas.
Na imagem abaixo, em qual foto é mais fácil saber a quantidade, professora?

A segunda foto facilita a contagem porque o grupo grande de ovelhas da primeira foto foi desagrupada em grupos menores de 3 ovelhas cada.
Para contar, na primeira foto, temos que contar uma a uma.
Na segunda, podemos contar os grupos de 3 multiplicar ou somar para sabermos o total.
Se você observar a segunda foto, professora, verá que identificamos facilmente cada grupo de 3.
Isso se deve ao que se chama Senso Numérico.

A Pedagogia 1.5 é resultado de 20 anos de docência em uma Faculdade de Pedagogia e 10 anos de Iniciação Científica.
Uma aluna e um aluno, em momentos distintos, perguntaram como ensinariam matemática se não sabiam a disciplina.
Nascia o LAPAPIEF – Laboratório de Pesquisa para Ação Pedagógica Interdisciplinar no Ensino Fundamental.
O objetivo do Laboratório: trabalhar com alunas e alunos a matemática. A síntese é o curso As Quatro Operações Matemáticas Fundamentais.
Descubra o Segredo Que se Esconde Por Trás do Senso Numérico
Na fotografia 2, acima, constata-se uma faculdade existente tanto em humanos quanto animais: a capacidade de, com uma simples olhar, perceber uma quantidade.
Essa quantidade que pode ser percebida, sem contar, restringe-se aos valores de um a quatro. É o senso numérico.
Essa é uma percepção direta de pequenas quantidades concretas. Ao olharmos, professora, para essas pequenas quantidades de objetos concretos, não contamos apenas percebemos quantos são.
Contar é algo abstrato. Essa é uma capacidade apenas humana. Alguns animais possuem senso numérico.
Certas mães animais mostram pelo seu comportamento que percebem se um ou alguns filhotes foram tirados dela.
“Assim, certas espécies animais são mais ou menos dotadas da noção de número, mas está encerrada em limites muito estreitos, encontrando-se reduzida ao que uma percepção imediata permite conhecer de uma olhada só.” Afirma Ifrah (1997, p. 6).
Os bebês humanos não possuem o senso numérico muito desenvolvido. Mas eles possuem a noção de número. Possuem um cérebro apto para desenvolver a noção de número.
Um animal não aprenderá a contar, professora. A criança, sim, irá construindo a noção de número pouco a pouco.
Com o senso numérico se consegue perceber a unidade, agrupamentos de dois, grupos de três e conjuntos de quatro coisas.
Diante de uma grande quantidade, para sabermos quantos elementos estão agrupados, precisamos ir desagrupando.
Contar, na realidade, é desagrupar um a um, dois a dois etc.
Como vimos na imagem acima, professora, uma quantidade maior que o senso numérico, agrupada, dificulta a contagem.
Nosso olho não consegue descobrir a quantidade em uma grande grupo, e para contar precisamos de algum mecanismo que nos ajude a avaliar quantos elementos estão no grupo.
Os egípcios usavam até nove traços para indicar nove unidades: IIIIIIIII. Observe, professora, que nossos olhos se perdem diante dessas traços enfileirados e fica difícil avaliar sua quantidade.
Para resolver essa situação, os egípcios desagrupavam os traços de acordo com o senso numérico: IIIIIIIII = III III III ou I IIII IIII, facilitando a percepção direta e a contagem.
Como o Ser Humano Pré-Histórico Avaliava Uma Grande Quantidade Sem Saber Contar?
A capacidade humana inventou uma maneira de saber a quantidade antes da criação da contagem abstrata que efetuamos de forma bastante natural hoje em dia.
O ser humano do neolítico, quando deixou de ser nômade e se fixou em determinado território e passou a domesticar animais e a plantar, inventou a comparação entre dois grupos de seres ou objetos: a correspondência um a um.

A imagem ilustra o pastor conferindo sua quantidade de ovelhas. Ele utiliza a correspondência um a um: para cada ovelha uma pedra.
Este artifício criado na Pré-História continua válido ainda hoje. Para que não se venda mais ingressos que o número de cadeiras em um teatro, o bilheteiro usa um mapa e vai assinalando os lugares vendidos.
O ser humano pré-histórico fazia aritmética embora os números, que são abstratos, ainda não tivessem sido criados. Ele usava como mecanismo a correspondência um a um a comparação entre objetos concretos, entre dois grupos, concretos.
Apesar de emparelhar dois grupos concretos, o processo, em si, é uma operação mental. Quer dizer, é abstrato, uma relação que se processa na mente.
Esse procedimento evoluiu para uma abstração maior. Do emparelhamento de pedras com objetos, alguém teve a ideia de entalhar riscos em madeira, osso ou argila. Cada traço correspondente a um objeto: um traço para cada ovelha, por exemplo.

A imagem é um osso de lobo com 18 cm de comprimento foi encontrado na República Tcheca, e datado de 30.000 anos atrás contendo traços, registros, de quantidade.
Vários povos usaram materiais diversos para a correspondência um a um: além das pedras, conchas, grãos diversos, bolas de argila pequenas, dentes de animais etc.
Mas o ser humano traz em sua anatomia as mãos com 5 dedos cada.
Esse detalhe anatômico provavelmente foi um dos primeiros recursos de correspondência um a um: um dedo para cada objeto.
Porém, não só os dedos das mãos, mas os dedos dos pés, as falanges de todos os dedos e diversas partes do corpo foram utilizados para aumentar a quantidade a ser registrada.
Qual a Mais Antiga Máquina de Calcular do Mundo?
Evidentemente, as mãos. Em povos de todos os continentes geográficos – mostram a arqueologia, a etnologia, a fonologia, a história – se encontram os traços das mãos como forma de contar.

A origem da palavra dedo é latina e é dígito. Na Aritmética, dígito significa cada um dos dez algarismos hindu-arábicos de 0 a 9.
Esse traço etimológico, parece tornar evidente a origem da contabilidade da espécie humana: as mãos com seus dedos.
Lembremos, professora, que as mãos são agrupamentos de 5 dedos cada.
Apesar de “estar sempre a mão” para a contagem, os dedos não são apropriados para memorizações e registros das quantidades.
“De toda forma, a mão do homem possui inúmeros recursos […]. Constitui uma espécie de ‘instrumento natural’ particularmente desenhado para a tomada de consciência dos dez primeiros números e da aprendizagem da aritmética elementar.”, escreve Ifrah (1997, p. 42).
As mãos são iguais, porém, simétricas, pois os dedos polegares são opostos. Deixam bem evidente os outros dedos, quatro em cada mão: lembra, professora, o senso numérico.
A mão contempla também os dois aspectos inerentes ao número: o ordinal e o cardinal, pois podemos contar 1, 2, 3 dedos; ou primeiro, segundo ou terceiro dedo.
Para se contar, é necessário perceber essas duas características do número que estão invariavelmente interligados: o ordinal e o cardinal.
Relembrando que a necessidade de contar está ligada a grupos. A unidade não precisa ser contada. As unidades de um grupo, sim.

Em frente a um prédio eu conto os números de andares, 1, 2, 3, 4, 5, 6 e falo aquela é a janela do apartamento de minha amiga, no quinto andar.
Ou diante de várias pessoas, pergunto: quem é o seu irmão? Você, provavelmente, contará: 1, 2, 3, 4, e responderá: é o quarto.
Os algarismos são os nomes das quantidades. Se conto 5 bolas, cinco é o nome do total de bolas naquele grupo: é o aspecto cardinal.
Já ordinal significa o lugar, a posição de determinado objeto ou elemento em uma sequência, relembrando, professora, a diferença entre ordinal e cardinal.
Quando a criança consegue estabelecer a diferença entre 6 brinquedos e o 6º brinquedo, ela deu grandes passos na construção do número.
Deseja Ensinar Seu Aluno a Não Errar Contas e Não Sabe a Melhor Maneira? Aprimore o Conhecimento Dele do Valor Posicional
Um dos motivos que levam os alunos a errarem as contas é não terem claro o Valor Posicional do algarismo.
Isto é, não saberem direito que o lugar que o algarismo ocupa no número determina seu valor: unidade, dezena, centena etc.
Isso é determinante para que ele entenda o “vai um”, ou seja, a conta com reserva.
Para a criança, não fica claro o que significa esse “vai um”. Na verdade, há um equívoco nessa expressão. Uma confusão entre o valor absoluto e o valor relativo do algarismo.
No numeral 333, qualquer dos três algarismos tem o valor absoluto 3. O valor absoluto não tem relação com a posição, o lugar, que o algarismo ocupa no numeral.
Numeral? Qual a diferença entre numeral e número, se perguntam os alunos?
Número tem a ver com quantidade: o número trinta e três é representado pelo numeral 33. Ou seja, numeral é representação gráfica do número.
No cotidiano, não fazemos essa distinção e chamamos numeral de número.
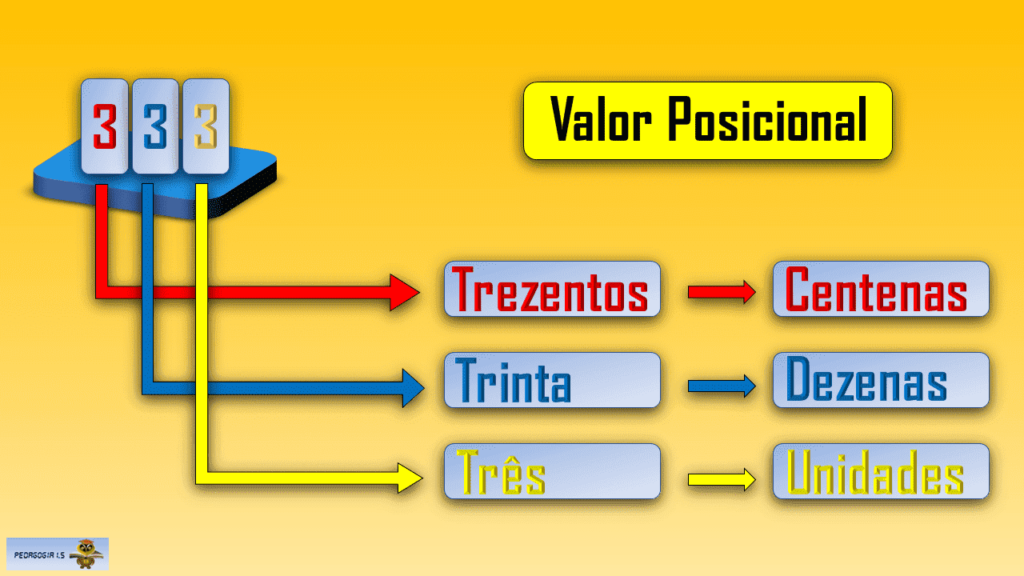
O valor relativo do algarismo depende de seu lugar, da posição que ocupa número. Quando falamos trezentos e trinta e três, a pronúncia do numeral 333, fica claro o Valor Posicional de cada algarismo 3.
O primeiro 3 vale três centenas, o segundo, trinta, três dezenas e o terceiro, três unidades.
Quando dizemos numa conta “vai um”, estamos usando o valor absoluto do algarismo e isso é um equívoco por não deixar claro para o aluno seu Valor Posicional.
Seria melhor que se dissesse, vai uma dezena. Assim o aluno levaria em conta o Valor Posicional e entenderia de forma mais evidente o que significa a expressão.
Compreenderia que estaria fazendo uma troca, transportando não o um, mas a dezena.
Para deixar ainda mais transparente para o aluno, professora, os numerais 41 e 14 são compostos pelos mesmos algarismos 1 e 4.
Porém, o Valor Posicional do 4 em quarenta e um é quatro dezenas e o 1 é uma unidade.
Em quatorze, o 1 vale uma dezena e o 4 tem o valor de 4 unidades.
Percebe, professora, que esse conhecimento liberta o aluno da ignorância e o auxilia a efetuar as contas com compreensão e propriedade.
A Maneira Mais Eficiente Para Seus Alunos Não Errarem Mais as Contas de Matemática
Aprender 3 dos Pilares do Ensino Orgânico em Matemática que são o agrupamento, o Valor Posicional e o Sistema de Numeração Decimal (SND) garante não errar as contas.
Falar é fácil, fazer é difícil, comenta o ditado. Como ensinar esses três pilares de forma orgânica?
Para isso, existe uma ferramenta que você já usa, professora: a Pedagogiação. Se você está lendo este artigo, você faz seu uso.
Atividades do Pinterest usam essa ferramenta. É uma forma consciente e intencional de ensinar Matemática.
Porém, professora, os seus alunos continuam a errar as quatro operações matemáticas fundamentais. Por quê?
Falta o Ensino Orgânico. E a melhor forma de Ensino Orgânico, ÚNICA, INOVADORA e REVOLUCIONÁRIA é a Pedagogiação1.5.
A Pedagogiação1.5 é a ação pedagógica cientificamente orientada, consciente, intencional e orgânica.
Não deixamos de insistir sempre, professora: acorde a Cientista da Educação adormecida que está em você.
Você não estudou Pedagogia? Pedagogia não é a Ciência da Educação? Então você se tornou uma cientista ao passar pelo rito de passagem de sua formatura.
Quer ver a Pedagogiação1.5 funcionando na prática? Então baixe grátis o Minicurso Pedagogia1.5.
Nele, você, professora, terá uma amostra grátis de uma introdução ao ensino orgânico da Matemática. Principalmente de um de seus pilares que é o Agrupamento.
São 4 Vídeos-oficinas prontos para você utilizar com seus alunos em sala de aula, professora.
Por que vídeo, professora? Essa é a linguagem que seu aluno domina. Lembre-se que ele nasceu e pertence ao século XXI: já nasceu na era da Internet e da linguagem videográfica.
Essa linguagem ele entende muito melhor que a escrita e a falada.
Esse minicurso é uma amostra gratuita do Curso As Quatro Operações Matemáticas Fundamentais.
Esse curso usa como método a Pedagogia1.5: ÚNICO, INOVADOR e REVOLUCIONÁRIO.
Um método cuja principal ferramenta metodológica é a Pedagogiação1.5, a ação pedagógica cientificamente orientada, consciente, intencional e orgânica.
Veja depoimentos sobre o método aqui e se gostar do Minicurso, provavelmente, vai querer também o Curso As Quatro Operações Matemáticas Fundamentais. Veja agora mesmo.
Referências
IFRAH, Georges. História universal dos algarismos, volume I: a inteligência dos homens contada pelos números e pelo cálculo. Rio de Janeiro: Nova Fronteira, 1997.


