
OS SEGREDOS DO ÁBACO QUE VÃO AJUDAR OS ALUNOS DO EFI A NÃO MAIS ERRAR AS CONTAS NAS ATIVIDADES MATEMÁTICA
A história do ábaco ajuda a entender como se deu o desenvolvimento da história da Matemática. Entender o desenvolvimento histórico do ábaco, possibilitará ao aluno do Ensino Fundamental I entender que a Matemática é concreta e não puramente abstrata.
Continue lendo, professora, e veja o segredo por trás do ábaco que vai possibilitar que os alunos não errem mais as contas.
Por que os alunos do Ensino Fundamental I erram tanto as contas? É uma pergunta que você, professora, deve se fazer e, talvez, ainda não tenha uma resposta.
Você gasta muito tempo pesquisando atividades – como toda boa Cientista da Educação faz. Relembrando: Pedagogia é a Ciência da Educação, portanto, você, professora, é uma Cientista da Educação.
No entanto, seus esforços, ao pesquisar atividades de matemática para aplicar em sala de aula, parecem em vão.
Você, professora, ao contrário de alguns professores, sabe que seu aluno não é burro, mas não entende porque ele erra tanto as quatro operações matemáticas fundamentais.
Às vezes você fica desanimada com esses erros e, por momentos, se acha incapaz.
Cuidado, Esse Erro É o Responsável Por Seus Alunos do Ensino Fundamental I Errarem as Contas das Atividades Matemáticas
Entretanto, os erros dos alunos do Ensino Fundamental I não são de sua responsabilidade e nem porque ele é burro. O sistema de ensino tradicional se engana ao ensinar os algoritmos, as contas, da maneira como faz.
Por se encontrar no período das operações concretas, o aluno não consegue fazer as contas, pois ele precisa do apoio do concreto para operacionalizar as contas, como mostra os escritos piagetianos, há várias décadas.
Ele faz nesse período abstrações pseudoempíricas. Ou seja, seu pensamento só consegue operar abstrações se estiver apoiado no concreto.
As contas são uma técnica, professora, abstrações refletidas, e o aluno do Ensino Fundamental I ainda não tem maturidade biológica para operar essa forma de abstração próprias do período das operações formais.
Durante décadas os estudos piagetianos, teóricos e práticos, já alertavam para esse engano do sistema de ensino. E tudo isso, também, foi confirmado por estudos da Neurociência Cognitiva.

O cérebro do aluno do Ensino Fundamental I, neste período das operações concretas, ainda está em desenvolvimento, portanto ele não tem maturidade cerebral, biológica, para operar abstrações refletidas.
O cérebro humano leva quase três décadas para completar seu desenvolvimento que começa no embrião e termina ao final dos vinte anos.
As contas, os algoritmos, são, portanto, abstrações refletidas. Os alunos do Ensino Fundamental I fazem abstrações pseudoempíricas, pois seus cérebros ainda não têm maturidade biológica, por isso erram tanto as contas.
O segredo para resolver esses erros? Continue lendo, professora, e você verá que a história do ábaco vai ajudar a entender a necessidade de usar o ábaco em sala de aula para a evitar os erros nas contas.
O Que Você Pode Aprender Com as Pedras na História da Matemática
Estamos tão acostumados com os números que nem nos damos conta que eles foram uma invenção do ser humano com uma história que levou milênios para ser concretizada.
Estamos tão acostumados a fazer contas que não percebemos, também, a sua invenção milenar histórica.
Aliás, nem mais fazemos contas, pois carregamos conosco uma calculadora no nosso bolso concretamente materializada num aplicativo em nossos celulares. Quando necessitamos fazer uma conta, acionamos a calculadora e em segundos temos os resultados.
Porém, na infância da humanidade, professora, os seres humanos ainda não tinham inventado os números e não sabiam contar.
No entanto, contar, quantificar, é uma necessidade fundamental das pessoas. Quando o ser humano se tornou sedentário, ele precisou saber a quantidade das coisas.
Domesticar os animais trouxe a obrigação de se saber quantos animais havia no rebanho. Os pastores, ao buscar suas ovelhas, necessitavam assegurar se todas se encontravam ali.
As mãos, com por sua grande mobilidade, tornaram-se a primeira máquina de calcular para o ser humano.
Porém, somente possuímos dez dedos nas mãos, aos quais se juntam os dez que temos nos pés. Quantidades acima de vinte necessitam de artefatos para sua contagem.
Pedras e depois entalhes em ossos, madeiras, pedras, argila auxiliaram a guardar grandes quantidades na memória.
Todos os povos precisaram e criaram sistemas de numeração para contar e calcular valores: mesopotâmios, sumérios, hindus, chineses, gregos, romanos, egípcios, árabes, maias etc.
No entanto, professora, contar e calcular grande grupos de coisas obrigou os povos a aperfeiçoarem os meios de efetuar cálculos e contagem. E novamente as pedras foram empregadas.
As pedras, em montes, começaram a arte do cálculo. A palavra cálculo veio do latim calculus cujo significado é pedrinha.
Preste Atenção na Origem do Ábaco e Você Vai se Surpreender...
As pedras estão na origem das máquinas de contar mecânicas como os ábacos, instrumentos feitos para calcular quando os cálculos foram ficando mais e mais difíceis (IFRAH, 1997).
Os montes de pedras foram substituídos por colunas de pedras e passaram a se contar unidades, dezenas e centenas da direita para a esquerda.
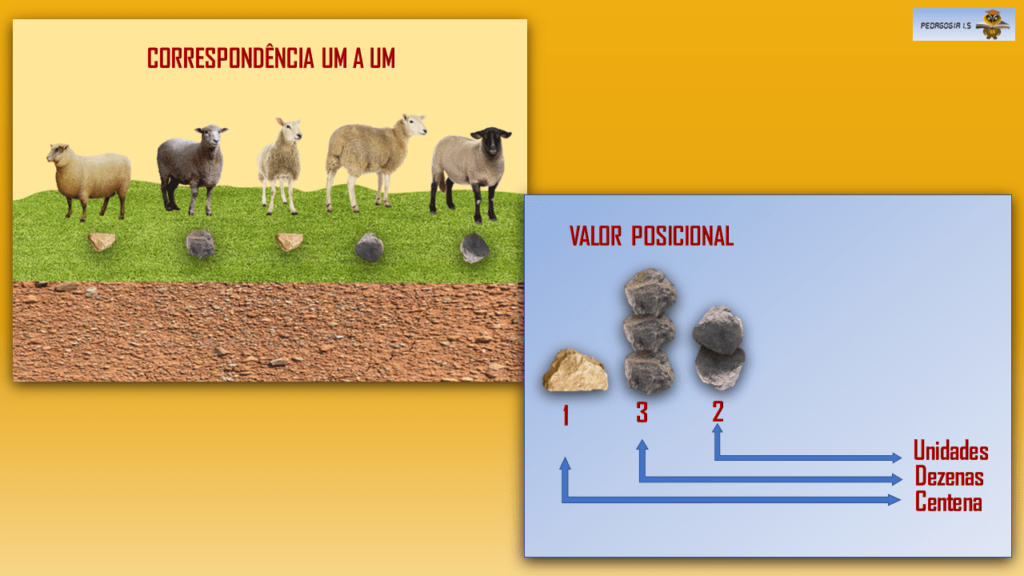
Depois, inventaram, as tábuas de contar: uma prancha que tinha diversas divisões com linhas formando colunas em que se colocavam pedras ou fichas.
O ábaco é um instrumento que possibilita efetuar as quatro operações fundamentais com números inteiros positivos e frações simples. O conceito de Valor Posicional está inconscientemente antecipado (REIS, 2011, p. 17).
A história humana, professora, ficou registrada em pinturas, pedras e artefatos pesquisados por antropólogos e paleontólogos. Registra, portanto, o ábaco como instrumento de contagem.
A autora informa que o ábaco surgiu por volta do III milênio a.C. e foi usado até o século XX. A palavra abacus provém do grego abakos cuja origem parece ser hebraica ibeq cujo significado é limpar o pó e abaq significando pó.
O sistema numérico Hindu-arábico se fundamenta no Valor Posicional e no símbolo para o zero, capaz de mostrar o lugar vazio, foi um dos grandes inventos da humanidade, possibilitando que a matemática, a aritmética, avançassem muito.
Porém, eles só apareceram por volta dos séculos IV e V na Índia e foram transmitidos aos árabes a partir do ano 662.
Até então, o ábaco era o instrumento mecânico utilizado para a calcular as operações aritméticas.
Conheça De Perto a História do Ábaco
Reis faz um estudo histórico dos ábacos. Tem-se notícias do ábaco sumério que seria em argila ou areia, cerca de 2700 a 2300 antes de Cristo. Deve ter sido um quadro com colunas, mas não usava a base decimal como os que conhecemos, mas a base 60, o sistema sexagesimal.
O ábaco babilônio foi implantado perto do século XV a.C. O primeiro deve ter sido construído com uma pedra lisa sobre a qual se colocava uma camada de areia ou pó. Depois evoluiu para tábuas de argila fresca.
Para não precisarem memorizar os resultados nas multiplicações de maior complexidade, os abacistas, a partir do II milênio a.C., passaram a usar tábuas de multiplicação feitas em argila ou madeira.

O ábaco egípcio foi também contemporâneo do babilônio, porém, seu registro só foi feito por Heródoto, o historiador, no século V.
Os egípcios, apesar do caráter simples de sua numeração escrita, a utilizavam para efetuar operações aritméticas e conseguiam somar, subtrair e multiplicar por dez. entretanto, eram processos efetuados com lentidão e bastante complexidade.
Os gregos tinham um sistema de numeração similar ao egípcio, mas o simplificaram utilizando a base 5, de forma auxiliar. Como o sistema era muito complexo impossibilitava realizar qualquer cálculo.
As dificuldades para efetuar cálculos levaram tanto gregos quanto romanos a utilizarem mesas de contar ou ábacos.
A arqueologia estuda objetos antigos para buscar conhecimentos novos a respeito daquilo que desconhecemos sobre o passado.
A tábua de Salamina, uma ilha grega, foi descoberta em 1846, representa o mais antigo ábaco que se conhece, datado de 300 a.C. Peça de mármore mede 75 cm de largura, 149 de comprimento e 4,5 de espessura. Cada coluna representa ordens de unidades.
O ábaco grego aparece em uma peça arqueológica, (um vaso) da época persa do Rei Dario, em que dois homens estão sentados próximos a uma mesa de cálculo. Essas mesas eram de mármore ou madeira e sobre elas usavam-se fichas miúdas de metal ou osso.

A autora ainda nos informa sobre outro tipo de ábaco de areia ou pó utilizado por gregos, persas e romanos, descrito no século II a.C., por Plutarco, consistindo numa tabuleta cujas extremidades eram levantadas e preenchido com areia fina em que se faziam colunas e se traçavam algarismos com uma ponta de ferro ou os dedos.
Saiba Exatamente Como os Algarismos Indo-Arábicos Foram Usados Com o Ábaco
Atualmente, usamos os algarismos arábicos que surgiram na Índia por volta dos séculos IV e V.
Entre os séculos V e VI, os algarismos indianos chamados brahmî evoluem para o Valor Posicional fundamentados na base dez e possibilitam efetuar cálculos aritméticos com o acréscimo do símbolo do zero.
Reis informa que, por volta do ano de 662, esses algarismos foram difundidos entre os árabes da Síria e depois entre os europeus.
Os padres e soldados que voltavam das Cruzadas, além das trocas comerciais, possibilitaram a difusão pela Europa da numeração hindu-arábica.
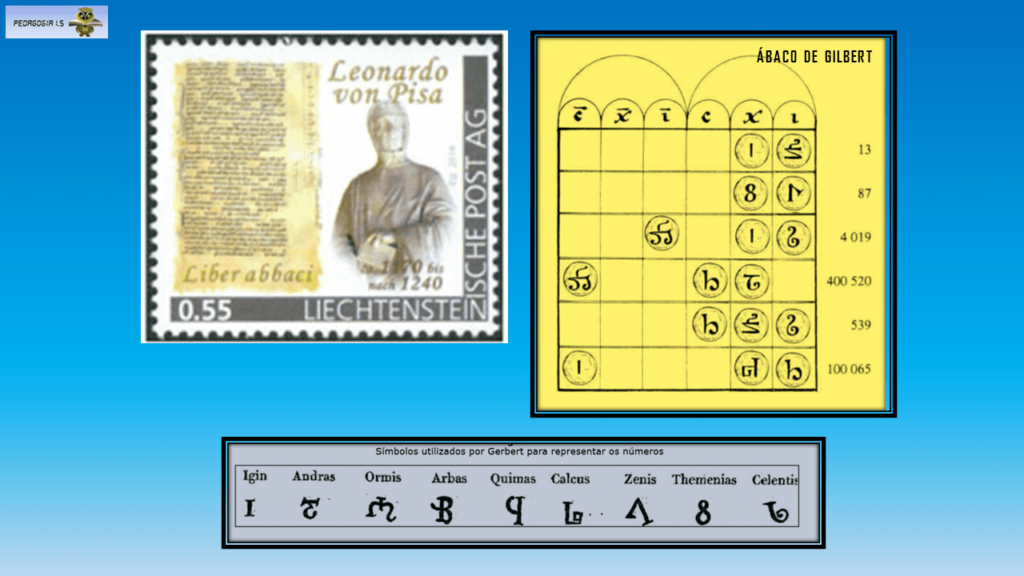
Um professor de teologia, Gebert d’Aurillac (depois Papa Silvestre II), no séc. X, aprendeu a numeração hindu e a nova metodologia de calcular levadas pelos árabes.
Foi um dos responsáveis pela sua introdução na Europa. Ele ensinava por meio do ábaco de Gebert, uma sua inovação do ábaco romano.
Autor de vários livros, era estudioso da Matemática e seus contatos com os mulçumanos ajudou-o na aquisição desses conhecimentos, elaborando novos métodos de multiplicação e divisão a partir do ábaco.
Gebert passou a usar o ábaco juntamente com os algarismos hindu-arábicos o que tornava o manuseio do ábaco mais complexo, pois saia do concreto (o uso das pedras) para o abstrato (os algarismos). (ALBUQUERQUE; PEREIRA; ALVES: 2018).
O Que Todos Devem Saber Sobre o Surgimento dos Algarismos Indo-Arábicos
Já em 1202, Leonardo de Pisa escreveu o Liber Abaci em que apresentava essa nova maneira de calcular usando os nove algarismos mais o zero.
Ele destaca sua grande vantagem para as pessoas encarregadas do comércio e que necessitavam fazer operações aritméticas.
Mas sua divulgação não foi tão simples e, até metade do séc. XIII, somente pequena parcela do povo entendia essa nova forma de calcular.
O preconceito dificultou a divulgação e utilização do sistema de numeração hindu-arábico trabalhada por Gebert. Espíritos conservadores, imbuídos da ideologia católica, rejeitavam os ensinamentos por provirem dos árabes.
Os cálculos aritméticos eram sobremaneira difíceis, mas os algarismos hindu-arábicos os facilitavam. Por isso, eram vistos como coisa demoníaca e Gebert foi visto como bruxo que havia aprendido bruxarias com os infiéis árabes e vendido sua alma a Lúcifer (COSTA, 2009).
As Cruzadas desempenharam um papel fundamental na divulgação dos novos conhecimentos matemáticos.
Quase dois séculos de guerra, em que os ocidentais, por meio da guerra, tentavam impor suas crenças religiosas aos orientais mulçumanos.
O contato entre eles efetivou um efeito contrário: foram os ocidentais que acabaram por absorver os conhecimentos e culturas dos mulçumanos, entre eles os conhecimentos matemáticos.
Em 1228, Fibonacci, um matemático ligado ao cristianismo, lançou uma segunda edição do Liber abaci que, desde a primeira edição, fornecia a seus contemporâneos uma detalhada e clara explicação da arte do cálculo que havia sido desenvolvida pelos árabes.
Nessa segunda edição, revisada, havia sido retirado o supérfluo e, além dos algarismos indo-arábicos com explicações para se aplicar comercialmente, acrescentou problemas geométricos e algébricos.
A partir desse momento uma nova era das operações matemáticas e cálculos começa para o mundo ocidental.
Por que o Ábaco Foi Abandonado?
Os algarismos indo-arábicos, professora, e sua metodologia de cálculo passam a ser usadas nos problemas do dia a dia e propiciam a democratização do cálculo no mundo europeu.
Por esta época havia duas classes de calculadores: abacistas e, os mais novos, algoristas. Os abacistas eram hábeis no manejo dos ábacos e os algoristas hábeis no manuseio dos algarismos indo-arábicos.
Os abacistas tinham se tornado uma poderosa casta de profissionais do cálculo ligados à Igreja Católica detentora do poder naquele momento.
A ideologia foi um empecilho para a utilização do sistema de numeração indo-arábico no Ocidente. As autoridades clericais abominaram e faziam enormes críticas aos algarismos indo-arábicos.
Sua argumentação baseava-se na facilidade e engenhosidade do cálculo e diziam, se assim era, deveria ser algo mágico ou quem sabe demoníaco, sendo, portanto, coisa do diabo.
A Igreja, professora, chegou a julgar alguns algoristas e quase os mandou para a fogueira. O lado ideológico fundamentava-se no fato da Igreja manter o monopólio do ensino do cálculo e os algarismos indo-arábicos levavam a sua popularização e democratização.
A sua proibição pela Igreja impediu que o cálculo avançasse com maior velocidade. Porém, os mercadores faziam uso dele como se fosse um código secreto.
Porém, a sua democratização não pode ser evitada pela Igreja e ele foi se disseminando, pois a população que não tinha acesso a qualquer tipo de cálculo começou a utilizá-los.
Ainda de acordo com Costa (2009), o uso do ábaco persistiu durante vários séculos entre financistas, banqueiros, comerciantes e funcionários. A Revolução Francesa pôs um fim a sua utilização ao proibir que fosse usado nas administrações e escolas.
A expansão comercial europeia em grande escala possibilitou a resistência a favor dos algarismos indo-arábicos sendo mais forte que o preconceito contra a cultura árabe.
Os algarismos indo-arábicos se propagaram também devido a sua eficiência e eficácia. Primeiramente, devido a sua virtude econômica. As transações comerciais se fazem com maior velocidade e facilidade, principalmente, no controle de estoques.
Em segundo lugar, professora, os cálculos astronômicos foram enormemente facilitados e propiciaram o avanço das grandes navegações referentes aos séculos XIV e XV.
A luta entre abacistas e algoristas teve duração de alguns séculos: do XI ao XV. Os numerais indo-arábicos foram colocados na clandestinidade, pois eram proibidos em documentos oficiais.
O século XVI vai assistir o triunfo dos algoristas e o ábaco perde sua hegemonia e foi abandonado quando a Revolução Francesa o proibiu.
O Uso das Contas Com Algarismos Indo-Arábicos Foi Bom ou Ruim? Descubra Agora
A vitória dos algoristas, professora, democratizou o cálculo e estava de acordo com os ideais da Revolução Francesa em que predominava a burguesia, já que o capitalismo necessitava de meios mais eficientes e eficazes de cálculos.
Os algoristas trabalhavam uma técnica, uma receita, um passo a passo, que seguido à risca, possibilita não errar cálculos.
Essa técnica, porém, foi uma longa evolução dos métodos de calcular, sintetizadas, professora, pelos hindus e árabes.
Os cálculos aritméticos deixam de ser concretos para se transformarem em algo abstrato, pura técnica mental. É abstração refletida.
Os cálculos feitos pelos abacistas, ao contrário, apoiavam-se no material concreto que é o ábaco. É abstração pseudoempírica.
Sabia, professora, que você pode, ludicamente, criar ábacos com seus alunos?
Acompanhe no link como construir um ábaco com seus alunos.
Atalho Que Você Pode Usar Imediatamente Para Que Seus Alunos do Ensino Fundamental I Não Errem Mais as Contas
Pedagogiação.
O que seria a Pedagogiação?
Você, professora, que pesquisa atividades no Pinterest, está fazendo Pedagogiação. No entanto, essa é uma ação pedagógica somente consciente, intencional, porém, inorgânica.
Por que inorgânica? Vamos comparar, professora, com a Pedagogiação1.5 para facilitar a compreensão.
A Pedagogiação1.5 é uma ação pedagógica, entretanto, cientificamente orientada, também, consciente e intencional, porém, orgânica.
Cientificamente orientada, por quê?
Está apoiada em quatro ciências:
1. Semiótica: que estuda os símbolos, os signos. Como a Matemática trabalha com números, que são símbolos, auxilia a entender os números semioticamente.
2. Psicanálise: uma das razões dos erros dos alunos do Ensino Fundamental I nas contas é a Ansiedade Matemática, e os preceitos da Psicanálise auxiliarão a diminuir os efeitos dessa ansiedade.
Usando, principalmente, a Educação Narrativa, a Ansiedade Matemática consegue ser minorada.
3. Psicogenética: o entendimento, professora, de que o aluno do Ensino Fundamental I está no período das operações concretas e por isso precisa do apoio de material concreto será um forte aliado seu.
A compreensão da necessidade de usar o material concreto, tendo em vista que faz abstrações pseudoempíricas próprias desse período.
4. Neurociência Cognitiva: a confirmação das pesquisas da psicogenética piagetiana pela Neurociência Cognitiva da imaturidade biológica do cérebro do aluno no período das operações concretas possibilita repensar a forma de ensino tradicional.
Com a Pedagogiação1.5, você, professora, compreenderá precisamente a forma de agir, já que seu ensino-aprendizagem será encaminhado cientificamente e orientado de maneira que você saberá o caminho que seu aluno vai trilhar.
A Pedagogiação1.5 é a ferramenta principal do Método Pedagogia1.5. Um método Revolucionário, Único e Inovador.
A Pedagogia1.5 emprega como táticas Vídeos-oficinas com Leitura de Imagens (Fotografia, História em Quadrinhos, Publicidade, Pintura e Animação) para ensinar Matemática.
Esse método surgiu em um Laboratório de Iniciação Científica criado para alunas e alunos de Pedagogia: o LAPAPIEF – Laboratório de Pesquisa para Ação Pedagógica Interdisciplinar no Ensino Fundamental.
Mais de 10 anos de pesquisa nesse laboratório com alunos e alunos de Pedagogia produziram mais de uma centena e meia de planos de aulas inovadores.
Os fundamentos da Pedagogia1.5 estão ancorados em cinco pilares:
a) Educação Narrativa: o método usa a História da Matemática como fundamento e a Educação Narrativa será um forte auxiliar para ajudar minimizar os efeitos da Ansiedade Matemática dos alunos.
b) Agrupamento: a base das quatro operações fundamentais da Matemática é o Agrupamento. O método aprofunda o entendimento da soma e multiplicação como agrupar e da subtração e divisão como desagrupar;
c) Valor Posicional: um dos principais motivos dos alunos do Ensino Fundamental I errar as contas é o não entendimento do Valor Posicional. Eles não compreendem que o algarismo 3 em 33 tem valores diferentes conforme sua posição, o lugar que ocupa na numeração;
d) Sistema de Numeração Decimal (SND): Agrupamento e Valor Posicional estruturam o Sistema de Numeração Decimal. Portanto, o desconhecimento do SND leva os alunos a cometerem muitos erros.
e) Material Concreto: entre os materiais concretos utilizados pela Pedagogia1.5 estão os Vídeos-oficinas, pois as crianças e, logicamente, os alunos do Ensino Fundamental I são altamente alfabetizados na linguagem videográfica e isso facilita muito o processo de ensino-aprendizagem.
Veja, professora, os depoimentos dessas alunas e alunos que mostram o aprimoramento da/o Cientista da Educação nesse curso de Pedagogia, pois Pedagogia é a Ciência da Educação, então, evidentemente, você, professora, é uma Cientista da Educação.
Se você quer conhecer esse Método Revolucionário, Único, Inovador, ouse experimentar GRÁTIS o Minicurso Pedagogia1.5 que contém quatro Vídeos-oficinas prontos para que você possa utilizar em sala de aula com seus alunos.




