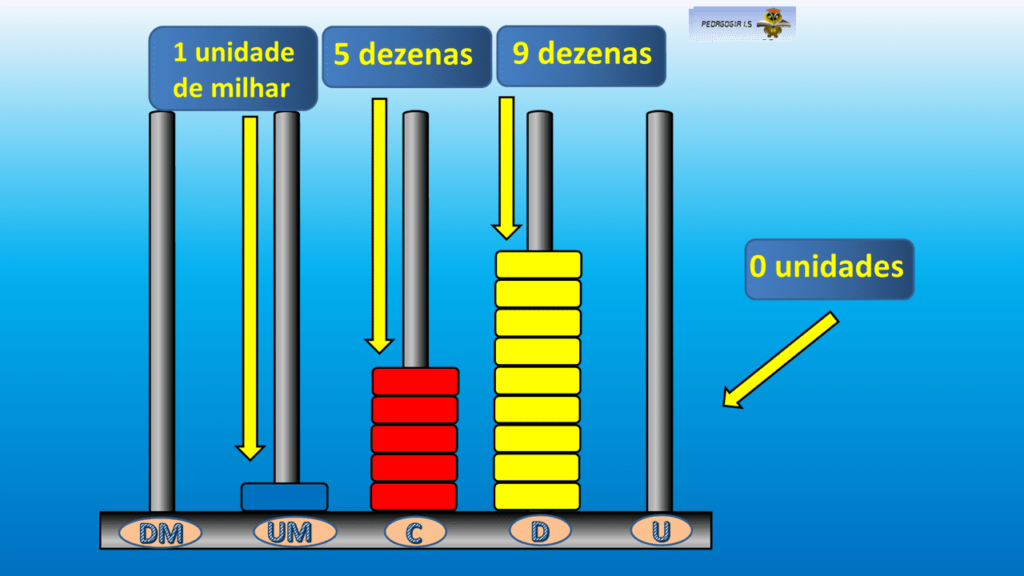
AQUI ESTÁ A FÓRMULA PARA ENSINAR SOMA COM RESERVA, O "vaI uM", SEM PRECISAR ESQUENTAR A CABEÇA: ÁBACO
Está difícil conseguir que seus alunos não errem as contas de somar com reserva?
As contas de somar com reserva causam muitos erros nas atividades de Matemática no 2º ano do ensino fundamental I. Neste artigo, vamos trabalhar a soma no ábaco e seu aluno nunca mais errará uma adição com reserva.
O ábaco, professora, é um instrumento utilizado por inúmeros povos há milênios.
Foi um artifício inventado pelo ser humano para facilitar a contagem e os cálculos.
A história da matemática mostra como o ser humano utilizou as mãos, as pedras, traços em ossos, madeira e argila para efetuar cálculos, para contabilizar grandes quantidades.
A história da invenção do ábaco é também a história da própria matemática.
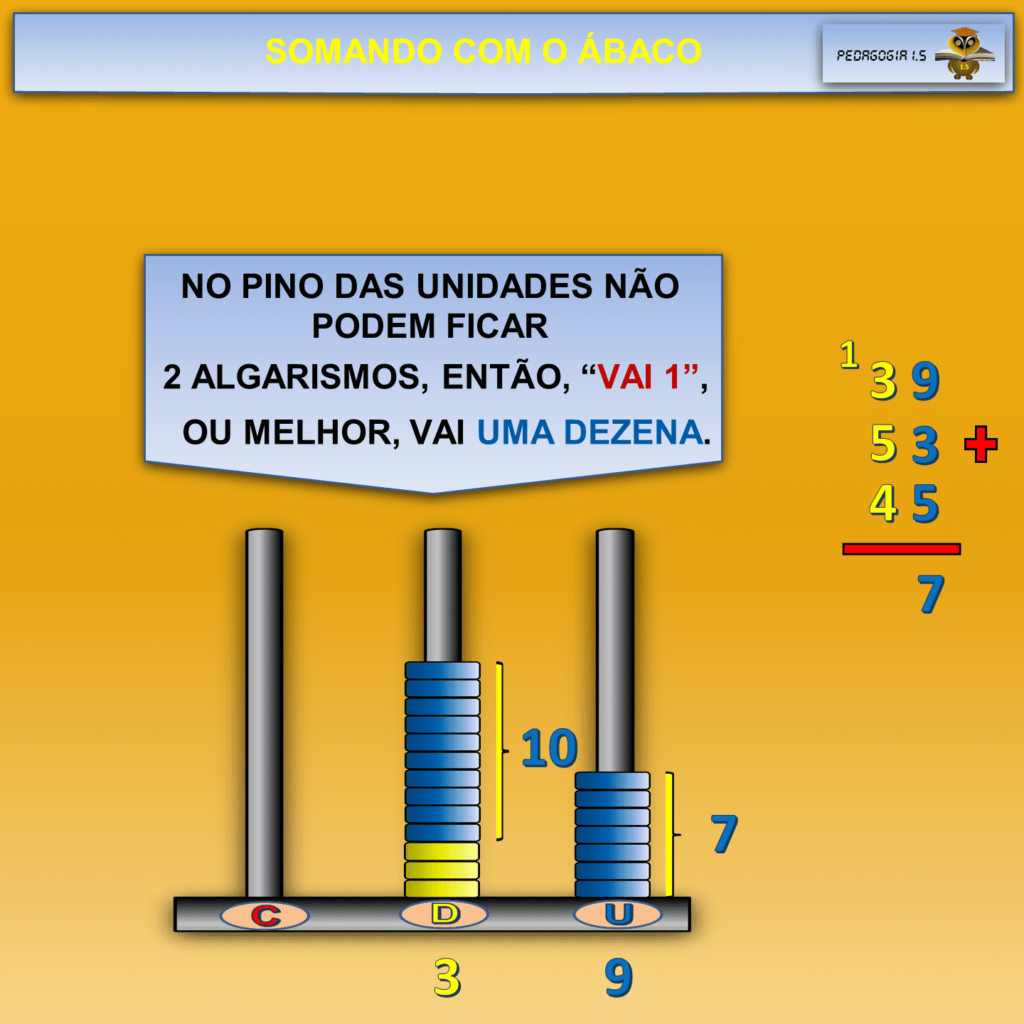
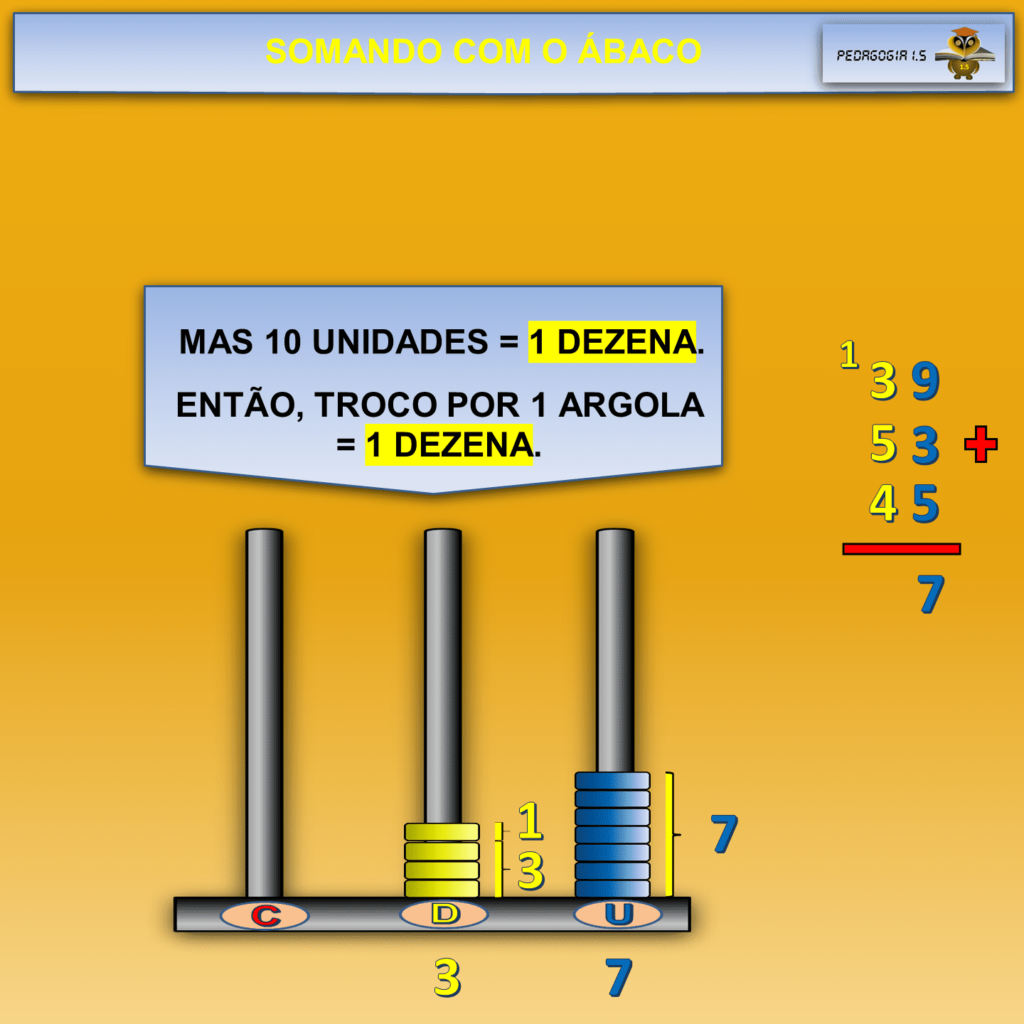
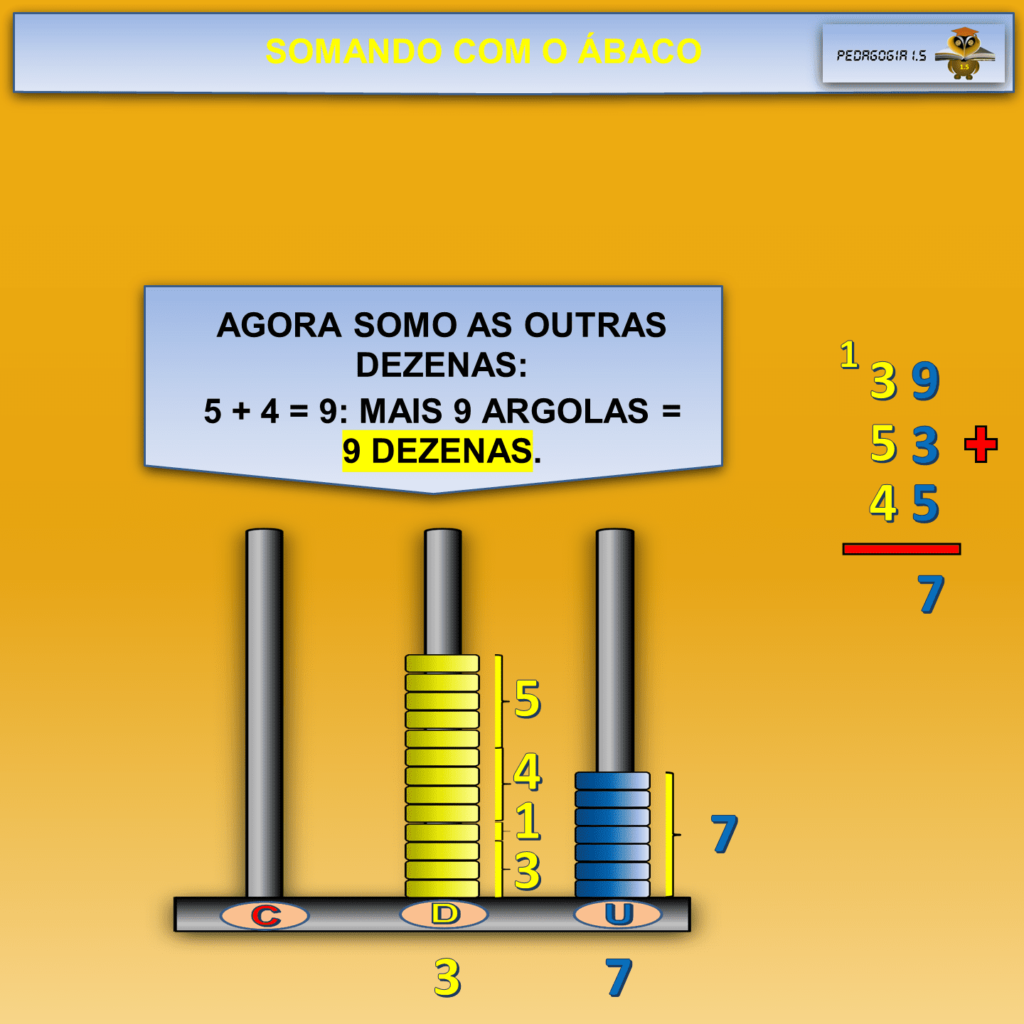
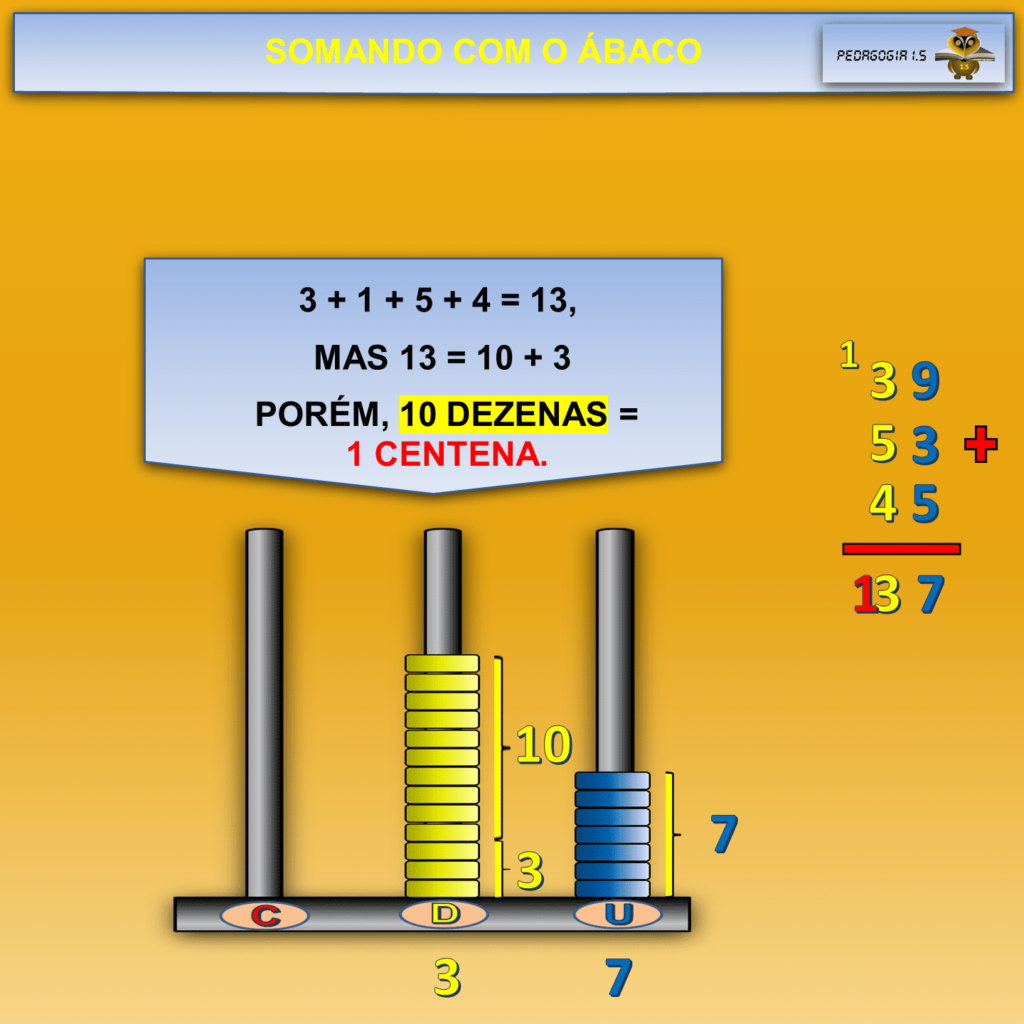
O ábaco possibilita materializar concretamente a abstração que é o “vai um” ou a adição com reserva.
Os alunos do Ensino Fundamental I, por estarem no período das operações concretas sentem enorme dificuldade para entender qual o motivo do “vai um”.
Por isso, Piaget recomenda o uso do ábaco. O “vai um” é uma operação formal que trabalha a partir da abstração reflexionante.
A criança do período operatório concreto opera a partir da abstração pseudoempírica, portanto, precisa do apoio do concreto para entender o processo da soma com reserva.
O “Vai Um”: Um Nó na Cabeça do Aluno
Professora, você já ouviu a expressão popular “deu um nó em minha cabeça”. O relato do William mostra exatamente o que o “vai um” é capaz de fazer na cabeça do aluno.
O “vai um”, para muitos alunos, funciona como um nó que trava seu aprendizado.
Por quê? Porque um nó paralisa. Uma dúvida não resolvida, paralisa o entendimento do aluno.
De onde saiu esse “vai um”? O aluno se pergunta. E como não consegue uma resposta fica paralisado na dúvida.
A partir do que vivenciamos no Laboratório de Iniciação Científica, no LAPAPIEF – Laboratório de Pesquisa para Ação Pedagógica Interdisciplinar no Ensino Fundamental – passamos a pensar em um nó epistemológico.
O “vai um” cria esse nó epistemológico. Episteme quer dizer conhecimento.
Então o nó epistemológico, professora, é um nó no conhecimento provocado pelo não entendimento da reserva, do “vai um”.
Como desatar esse nó, professora?
Para o aluno do Ensino Fundamental I, que se encontra no período das operações concretas, seu padrão de conhecer opera a partir da abstração pseudoempírica.
O ábaco é a ferramenta essencial para desatar esse nó epistemológico do “vai um”.
Neste artigo, professora, vamos exemplificar o uso do ábaco com uma adição. Isso possibilitará o entendimento de como opera a reserva, o “vai um”, na soma, deixando concreto esse processo tão abstrato do “vai um”.
A Palavra “Problema” É Um Problemão em Matemática
Como, também, trabalhamos a partir do Ensino Orgânico Narrativo, vamos usar uma história matemática para ilustrar a questão do “vai um”.
Você gosta de vivenciar um problema, professora? Conhece alguém que gosta de experenciar qualquer problema?
Acredito que não.
Esta argumentação encontra-se no livro Conversas sobre números, ações e operações de Luzia Faraco Ramos.
Ela alerta para o fato de que a vivência dos alunos com a palavra problema é bastante negativa.
Ela questiona se alguma vez uma criança ouviu qualquer adulto falar: Oba, estou com um problema bem legal para resolver.
Sugiro, professora, que pesquise em qualquer dicionário os sinônimos para a palavra problema. Verá que todas os sinônimos de problema são palavras de cunho altamente negativo.
Quando a palavra se une à Matemática, então, o problema fica muito maior.
Por isso, a autora, sugere que troquemos a palavra problema por histórias matemáticas ou outras expressões que não seja também situação-problema.
Dentro da perspectiva que trabalhamos de um Ensino Orgânico Narrativo, vamos trabalhar com Histórias Matemáticas, pois se adequa a um dos seus pilares que é usar a História da Matemática como uma das colunas de ensino-aprendizagem.
Pense, professora, o que acontece quando uma criança, desde bem pequena, vê seus pais conversando e ela ouve a palavra problema.
Como aprendemos os significados das palavras na língua materna? Eles vão sendo construídos na linguagem falada do dia a dia por meio da interação entre as pessoas, dialogicamente.
Ao contrário, a comunicação não verbal (a postura, os gestos, as expressões faciais, tons da voz) tem muito maior significação: captamos 70% da comunicação por esse meio, nos informa a Semiótica.
O que ocorre, portanto, quando a criança ouve a palavra problema? O contexto corporal e dialógico da palavra se expressa num tom de voz preocupado, negativo e o corpo reage de forma tensa ao significado da palavra.
A tensão corporal se expressa na postura, nos gestos, nas expressões faciais.
A criança, puro id, isto é, puro inconsciente, no pensamento freudiano, capta essa tensão inerente à palavra e cria todo um sentimento negativo em relação a ela.
Por isso, a Pedagogiação1.5 trabalha narrativamente, não com a palavra problema, mas Histórias Matemáticas.
A palavra história vem envolta por uma atmosfera de boas lembranças para a infância. Quem não gosta de ouvir histórias?
Não há, nunca existiu e jamais existirá um povo que não construiu, constrói e construirá histórias, seus mitos, suas lendas, sua indústria de entretenimento com seus filmes, novelas, seriados etc.
A aprendizagem dos problemas matemáticos são uma preocupação antiga.
Uma das maiores dificuldades encontradas pelo professor de curso primário é, sem dúvida, a de conduzir os alunos à resolução rápida e segura dos problemas aritméticos […] já afirmava Paiva e Souza na palestra O problema dos problemas.
Palavras com que iniciava sua fala, no século passado, em 1958.
A autora pondera que a escola, geralmente, usa uma linguagem descontextualizada dos problemas numéricos que trabalhamos no cotidiano.
Ela questiona: Quantas professoras terão levado para a sala de aula um jornal, uma revista, um livro, onde elementos numéricos aparecem entrosados em situações que merecem ser analisadas, trabalhadas, resolvidas. […]
Reconstruindo Um Problema Como História Matemática
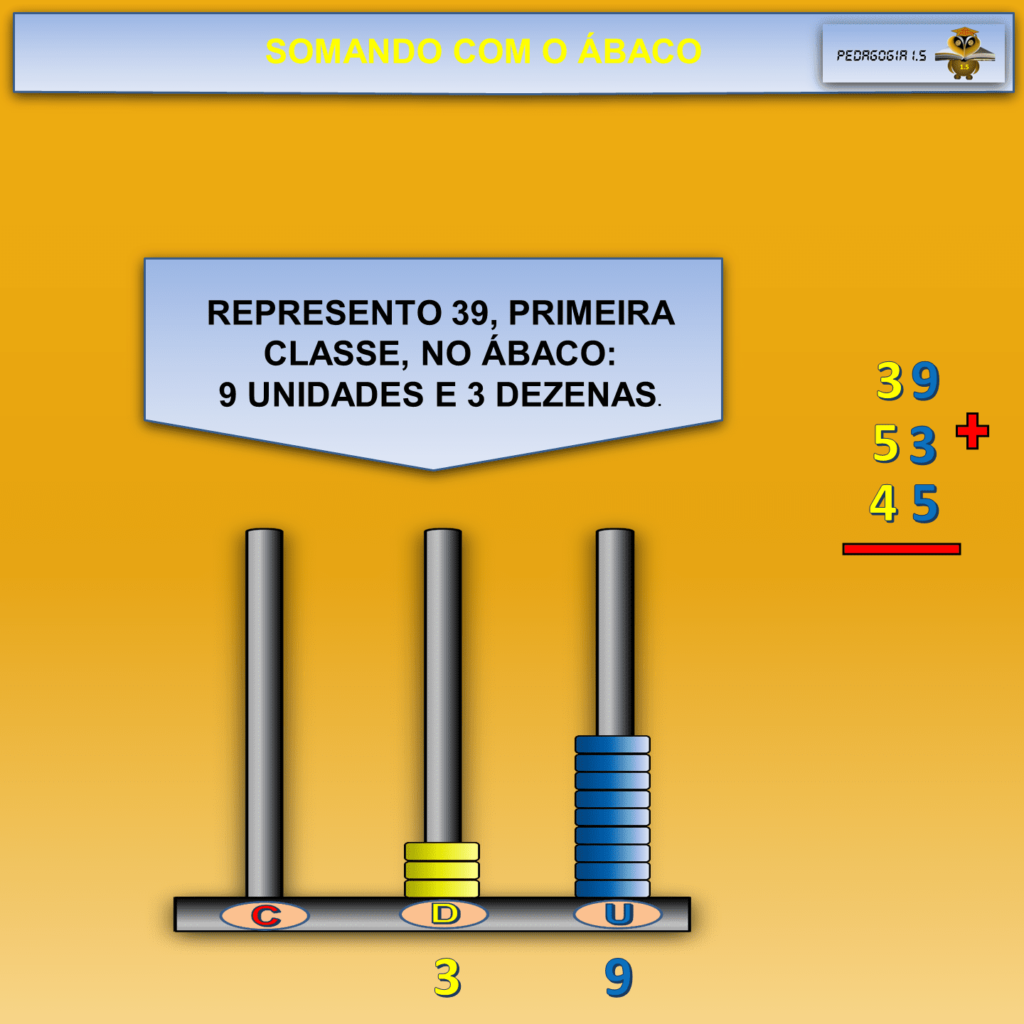
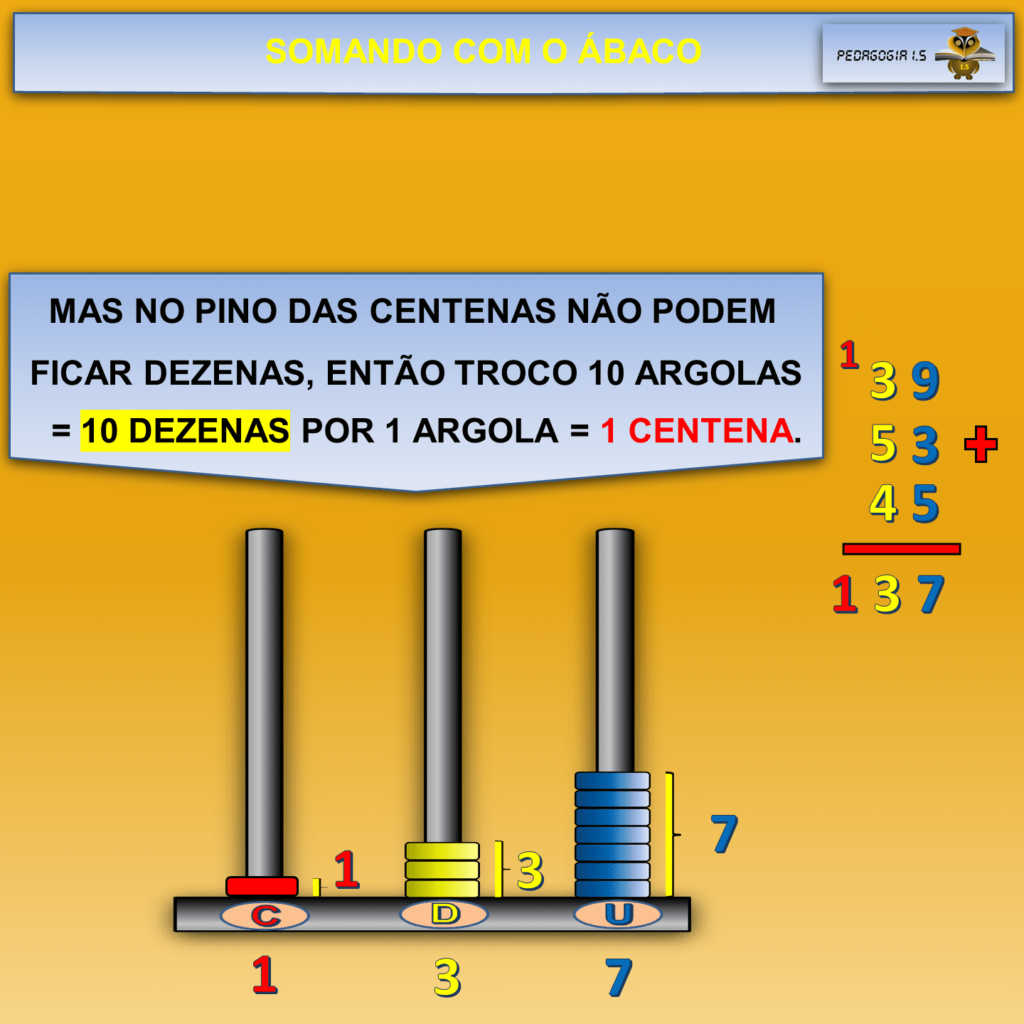
Uma escola está dividida em três classes: a pequena tem 39 alunos, a média 53 e a grande 45. Quantos alunos tem esta escola?
Este é um problema proposto por Lobo em sua Primeira aritmética – para meninos em 1954.
A linguagem do problema, por se ver como linguagem matemática, busca ser impessoal, fria.
Uma sugestão de reconstrução – História Matemática:
Uma escola de um bairro perto da minha casa está dividida em três classes: uma sala pequena tem 39 alunos, a sala de aula de tamanho médio tem 53 alunos e a sala de aula grande tem 45. Quantos alunos tem esta escola?
Professora, a transformação não foi grande, mas alguns dados fazem toda a diferença para o aluno:
1) Ao invés de problema, História Matemática: história é algo atrativo, lúdico, positivo.
2) Contextualização: escola de um bairro perto da minha casa. Tira a impessoalidade do problema e aproxima da vida cotidiana.
3) Na proposta de Lobo, omite-se a palavra classe que fica subentendida antes de pequena, média e grande. Os alunos têm que subentender.
4) Na reconstrução, a palavra classe é explicitada em cada situação para facilitar a leitura do aluno.
Usando UM Ábaco Para Resolver Esta História Matemática
O exercício prova que o ábaco facilita a compreensão da soma com o “vai um”.
E mais: os alunos erram muito as contas, não porque são burros, professora, mas em razão de não terem maturidade biológica para acompanhar o processo de abstração das continhas.
A Pedagogiação1.5 por isso mesmo pensa o ato pedagógico cientificamente orientado, mostrando que trabalhar com o material concreto, no caso o ábaco, possibilita ao aluno compreender a abstração própria da conta.
O ábaco torna a conta concreta, transformando toda a abstração desse processo em algo que o aluno possa compreender.
As dificuldades do aluno em entender a conta, principalmente o reagrupamento, o “vai um”, acontece porque o seu cérebro, no Ensino Fundamental I, ainda está em formação. É isso que nos mostra a Neurociência Cognitiva.
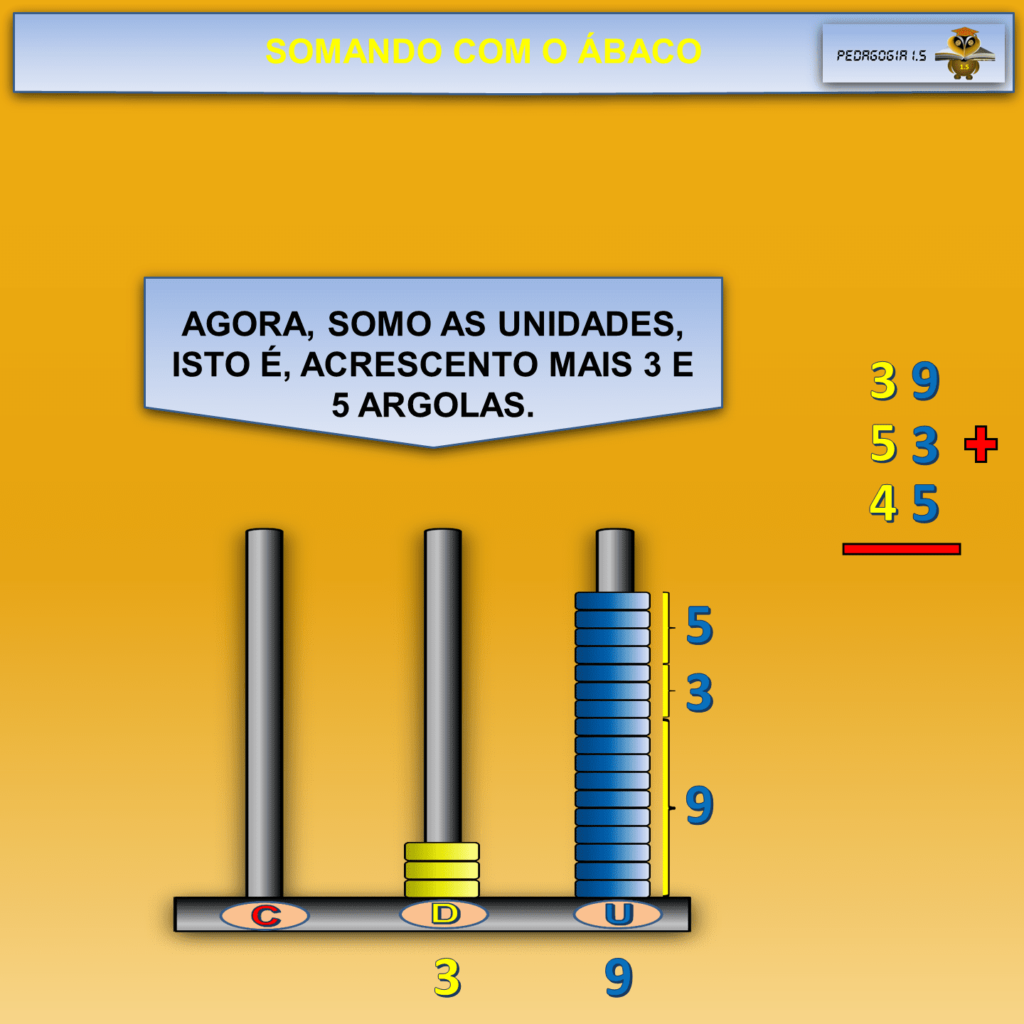
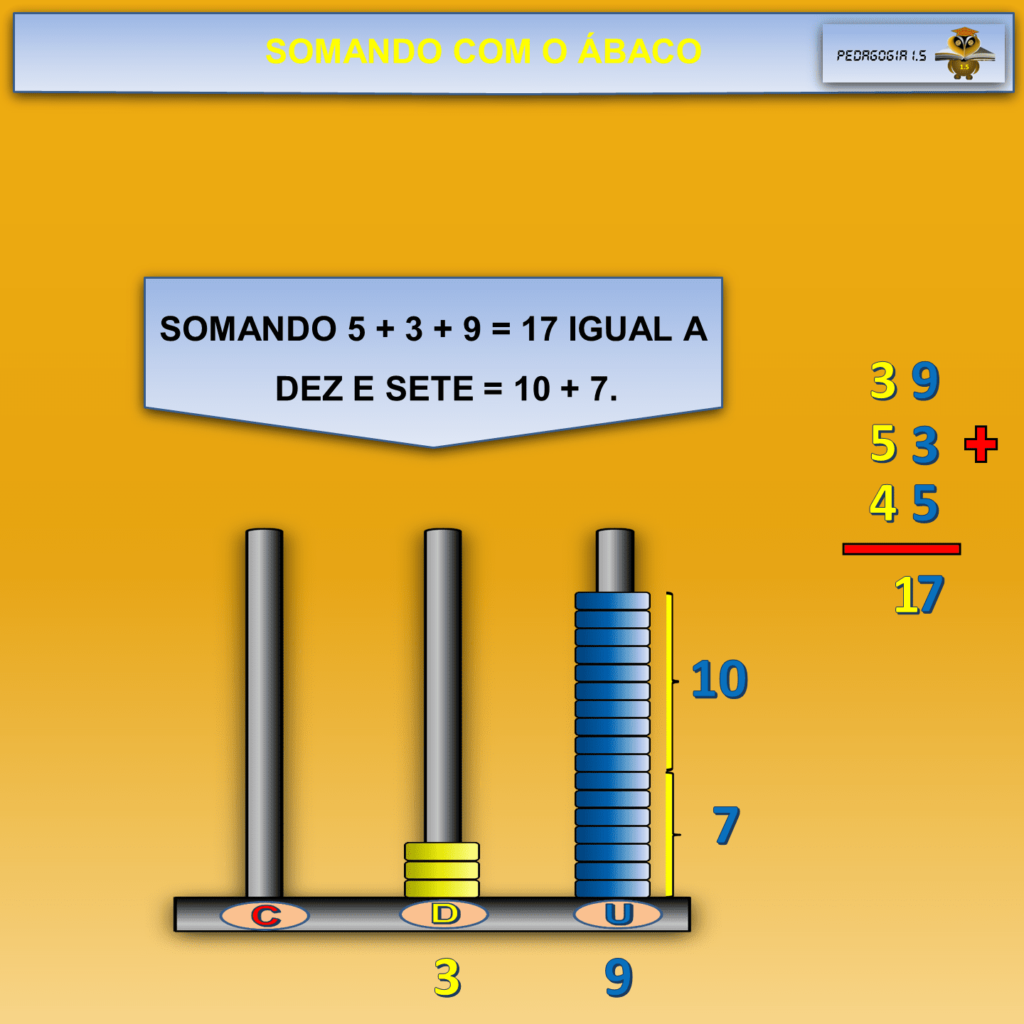
As argolas do ábaco auxiliam o processo de compreensão do aluno, pois ele soma concretamente 9 argolas mais 5 argolas e, como ele está no período concreto, faz abstração pseudoempírica como nos ensina o pensamento piagetiano.
A Neurociência Cognitiva veio confirmar a teoria das abstrações piagetiana e explicar a razão de o aluno do Ensino Fundamental I errar tanto as contas e, reafirmado: seu cérebro ainda não está completamente formado, por isso ele precisa do material concreto, no caso, o ábaco.
A Ferramenta Surpreendente Que Auxilia Você, Professora, no Processo de Ensino
Tudo isso, fica mais claro para você, professora, ao usar a metodologia da Pedagogia 1.5.
A Pedagogia1.5 usa a Pedagogiação1.5, a ação pedagógica cientificamente orientada, em que você tem acesso às orientações científicas da Semiótica, da Psicanálise, da Psicogenética e da Neurociência Cognitiva para guiar seu ato pedagógico.
Entre os materiais concretos que facilitam a compreensão do aluno, a Pedagogia1.5 aconselha e fornece Vídeos-oficinas como forma de facilitar tanto a compreensão do aluno como o seu trabalho em sala de aula, professora.
Se você, professora, quer experimentar a metodologia e estratégias da Pedagogia1.5 veja esse Minicurso GRATUITO com 4 Vídeos-oficinas prontos para você utilizar em sala de aula com seus alunos professora.