
A MELHOR FORMA DE EVITAR ERROS NAS CONTAS DE SUBTRAÇÃO NO 2º ANO DO EF1: USAR O MATERIAL DOURADO.
Erros nas contas de subtração ocorrem muito, principalmente, naquelas com reserva. Isso acontece, fundamentalmente, em razão do aluno desconhecer os princípios básicos do Agrupamento, Valor Posicional e Sistema de Numeração Decimal.
Por que isso acontece? Como resolver esse problema? Continue lendo, veja a razão e como solucionar usando o material dourado.

Errar as contas de subtração pode parecer natural, professora, porque a maioria dos alunos do 2º ano do Ensino Fundamental I erra.
Não é natural, professora, e veremos, no decorrer desse artigo, que há um equívoco do Sistema de Ensino.
Na vida cotidiana utilizamos a subtração de modo bastante natural. A noção de retirar algo de algum lugar: encher uma xícara de café significa retirar o café de um bule, por exemplo.
Se temos uma coleção de qualquer coisa, se falta uma ou mais peças, sentimos essa falta, pois foram retiradas da coleção.
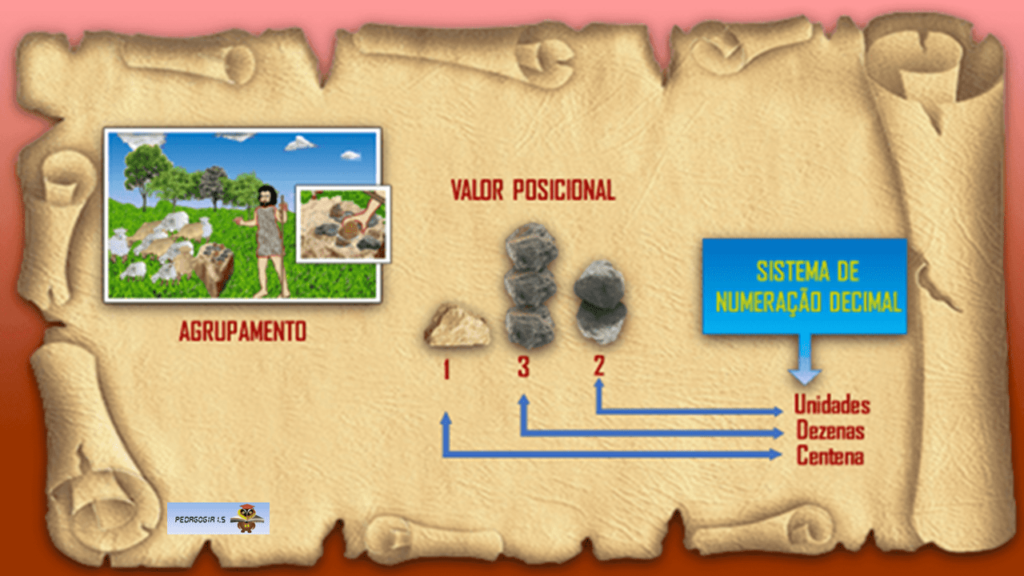
Na História da Matemática, exemplifica-se com a necessidade de pastores de ovelhas, verificarem, quando ainda não sabiam contar, e o número de ovelhas era maior se faltavam alguma em seu rebanho.
Essa necessidade de contar, contabilizar, levou o ser humano a criar artifícios para controlar as quantidades e verificar a falta de peças em um agrupamento de coisas.
As mãos foram a primeira máquina de calcular. Mas os dedos das mãos e dos pés são apenas 20, impossibilitando o controle de quantidades maiores que vinte.
Recorreu-se, professora, então às pedras, por meio da correspondência um a um, para controlar as quantidades: para cada ovelha, uma pedra.
Das pedras passou-se para a representação gráfica de traços em ossos, pedras, madeira, argila. Um traço representando uma unidade ou grupos de unidade.
Com o decorrer de vários séculos chegou-se à representação por meio de algarismos. Os números escritos foram criados para simbolizar quantidades.
O Segredo na História da Matemática Que Ajuda a Explicar Erros nas Contas
Os algarismos hindus são bem próximos dos algarismos que trabalhamos hoje. Os hindus criaram o zero, e essa criação facilitou o desenvolvimento do Valor Posicional em que um mesmo algarismo vale de acordo com sua posição, seu lugar no numeral.
Os árabes reconheceram a superioridade do sistema de numeração hindu e trabalharam a partir dele divulgando-o e levando ao abandono do sistema de numeração romano.
Al-Khuarismi, um matemático árabe que viveu entre os anos 780 e 850, levou aos europeus os algarismos indo-arábicos. Aliás algarismo vem do seu nome: Al-Khuarismi.
Al-Khuarismi escreveu em seu Livro de adição e subtração, de acordo com o cálculo hindu que se pode representar qualquer número usando apenas 10 algarismos: de 1 a 9 mais o 0, conceitos desenvolvidos pelos hindus por volta do século VI.
Essa foi uma ideia revolucionária e que facilitava muito o cálculo, já que efetuar cálculo com os algarismos romanos era muito complicado.
O Sistema de Numeração Decimal (SND) surge a partir dos algarismos indo-arábicos. Os hindus descobriram a importância do Valor Posicional em que a posição do algarismo no número é relativa, não importando seu valor absoluto.
Ou seja: um mesmo algarismo, 3 por exemplo, vale 3 unidades, 3 dezenas ou 3 centenas etc. de acordo com o lugar, a posição que ocupa no número.
Todo esse longo processo de construção do Sistema de Numeração Decimal, que facilitou o surgimento dos algoritmos, das contas, facilitou enormemente o avanço da Matemática e da tecnologia.
Trata-se de um processo bastante complexo e abstrato. O que é a conta, o algoritmo? É uma técnica, um passo a passo extremamente abstrato para se calcular. Porém, ele é muito eficiente e econômico. O domínio da técnica possibilita efetuar qualquer cálculo.
Sendo abstrato, porém, causa um inconveniente para os alunos do Ensino Fundamental I. Isso já nos alertava o pensamento piagetiano há várias décadas.
Professora, você se recorda dos períodos de desenvolvimento ensinados nos estudos piagetianos. A criança do Ensino Fundamental I encontra-se no período das operações concretas. Isso quer dizer que para operar ele necessita do concreto.
Ora, se a conta, o algoritmo, é um processo técnico muito complexo, abstrato, é natural que o aluno do Ensino Fundamental I erre tanto as contas, pois nesse período ele faz o que Piaget chama de abstrações pseudoempíricas.
Pseudo quer dizer falso. Empírico é aquilo vivido pela experiência, o que é observado. Então, pseudoempírico é um falso empírico. Por quê? Em razão de que o processo é abstrato, mas apoiado na experiência, no concreto.
A explicação que Becker apresenta desse conceito piagetiano é muito clara: se observamos uma maçã, essa é uma experiência empírica, uma abstração empírica. Observamos o objeto e constatamos: é uma maçã.
Entenda, Professora, a Razão da Necessidade de Usar Material Dourado
Estando no período operacional concreto, o aluno vai precisar de um material concreto para conseguir abstrair. E o material dourado é um material concreto estruturado.
Quer dizer, ele foi construído e estruturado para trabalhar unidades, dezenas e centenas. Isso possibilita ao aluno visualizar, materializar, concretizar o Sistema de Numeração Decimal (SND).
Maria Montessori criou o material dourado para ensinar crianças deficientes. O uso do material dourado por essas crianças mostrou que, com ele, elas competiam no mesmo patamar com as crianças não deficientes.
Montessori criou um material concreto para representar conceitos abstratos que se materializam para o aluno. Conceitos como Valor Posicional ganham uma dimensão concreta e podem ser visualizados pelos alunos.
Assim, a criança numa subtração em que precisa subtrair 9 menos 4, percebe, concretamente, empiricamente, que não é possível tirar 4 cubinhos de 9 cubinhos e consegue ver a necessidade de reagrupar, pois de 14 cubinhos, 10 + 4, consegue retirar os nove e visualiza que vai uma dezena ou uma barrinha.
Todos esses conceitos e ideias, professora, levam você a uma pedagogiação. E são explorados na Pedagogiação1.5 que é uma ação pedagógica orgânica, consciente, intencional, cientificamente orientada.
Relembremos, professora, que você é uma Cientista da Educação. Você é uma Pedagoga e, como a Pedagogia é a Ciência da Educação, logicamente…
A Pedagogiação1.5 é uma ferramenta da Pedagogia1.5: um método Único, Inovador e Revolucionário que pode auxiliar, você, professora, a utilizar novas formas de ensino para facilitar a aprendizagem de seus alunos.
A Pedagogia1.5 nasceu no LAPAPIEF – Laboratório de Pesquisa para Ação Pedagógica Interdisciplinar no Ensino Fundamental – um Laboratório de Iniciação Científica para alunas e alunos de Pedagogia.
Você, professora, pode ter uma amostra totalmente GRATUITA da Pedagogia1.5 e de sua ferramenta principal a Pedagogiação1.5 no Minicurso GRATUITO Pedagogia1.5.
Referências
BECKER, Fernando. Abstração pseudo-empírica e reflexionante: significado epistemológico e educacional. Shème: Revista Eletrônica de Psicologia e Epistemologia Genética, v. 6, Edição Especial, nov. 2014, p. 104-128. Disponível em: < https://revistas.marilia.unesp.br/index.php/scheme/article/view/4276 >. Acesso em: 02 mar. 2023.
PIAGET, Jean. Abstração reflexionante: relações lógico-aritméticas e ordem das relações espaciais. Porto Alegre: Artes Médicas, 1995.



