QUERENDO ENCONTRAR FORMAS DE SEU ALUNO DO 4º E 5º ANOS DO EFI NÃO ERRAR AS CONTAS DE DIVIDIR ?
As contas de dividir são uma das maiores fontes de erro dos alunos do 4º e 5º anos do Ensino Fundamental I.
Veja as razões, científicas, neste artigo, porque se deve usar o material concreto para o ensino-aprendizagem das contas, especificamente, o ábaco.
Você, professora, vive em busca de atividades diferenciadas para o ensino de contas de dividir, os algoritmos de divisão.
Por mais que se esforce, os erros nessas contas são constantes e muitas vezes você se sente desanimada e questiona seu processo de ensino.
Antenada como você é, sabe que não deve responsabilizar os alunos e muito menos agir como diversos professores que consideram burrice os erros nas contas de dividir.
A boa notícia, professora, é que há uma forma fácil de evitar esses erros e, melhor ainda, ao continuar lendo este artigo, você vai entender as razões que levam o aluno a esses erros.
Eles não são produtos nem de burrice do aluno nem há incompetência sua no ensino.
Os alunos do 4º e 5º anos do Ensino Fundamental I erram, principalmente as contas de divisão, porque seus cérebros ainda estão em desenvolvimento como comprova a Neurociência Cognitiva.
Essa ciência demonstra que a evolução do cérebro humano acontece por décadas. Só ao final dos vinte anos o cérebro completa seu desenvolvimento.
O cérebro do aluno nesse período do Ensino Fundamental I (EFI) não é capaz de fazer abstrações formais.
Tudo isso já foi devidamente estudado, tanto teórica como praticamente, pela Psicogenética piagetiana.
Nesse período, denominado estágio das operações concretas, os alunos fazem o que Piaget chama de abstrações pseudoempíricas.
Somos envolvidos por milhares de informações e alguma coisa nos chama a atenção. Ao olhar, por exemplo, para uma bicicleta e reconhecer esse objeto como bicicleta, na minha mente estou fazendo uma abstração empírica.
Dou o nome de bicicleta a esse objeto. Reconheço, isto é, entre milhares de outros objetos distingo características próprias desse objeto a que chamo bicicleta. Empírico quer dizer algo próprio da minha experiência, algo que vivencio.
Mas reconhecer é identificar algo que já se conhecia. Conhecer é aprender algo novo e guardar na memória. Tudo isso é abstração: conheço mentalmente; reconheço também mentalmente, isso é abstração empírica.
Nem todos que conhecem uma bicicleta vão dizer que ela é uma bicicleta ecológica. O adjetivo ecológico dá uma qualidade à bicicleta que pomos nela. A qualidade de ser um objeto que não polui como carros, aviões etc.
Ao darmos uma qualidade a um objeto, estamos fazendo uma abstração pseudoempírica, pois, apoiados no objeto, colocamos nele uma qualidade, que é mental.
Se vemos várias bicicletas, reconhecemos um agrupamento de bicicletas. Isso é abstração empírica, pois a experiência me mostra um grupo de bicicletas.
Se as bicicletas estiverem enfileiradas e eu contar, professora, uma a uma – e geralmente faço isso apontando com o dedo indicador, faço uma abstração pseudoempírica. Por quê?
Porque atribuo uma quantidade a cada bicicleta. Porém, é uma relação mental, estou atribuindo uma quantidade a cada objeto. Conto apoiado nos objetos, mas contar é uma operação mental.
Se uma criança conseguir contar as bicicletas de duas em duas e somar: 2 + 2 + 2 = 6 e ela perceber que 2 + 2 + 2 = 6 = 2 três vezes, ou seja, 2 x 3 = 6, ela fez uma abstração refletida.
Ou seja, ela refletiu sobre uma operação de soma e tomou consciência que essa operação pode ser uma multiplicação.
Abstrações refletidas são próprias do período das operações formais a partir dos 10 a 12 anos. O desenvolvimento cerebral desse período possibilita as tomadas de consciência.
O aluno dessa faixa etária consegue fazer operações mentais sem precisar se apoiar no concreto.
O que foi dito acima, professora, prova que há a necessidade de usar material concreto para ensinar as contas de divisão para os alunos do 4º e 5º ano do Ensino Fundamental I.
A Verdade É Que Ensinar Divisão Para Alunos do 4º e 5º Anos do EFI É Mais Fácil Usando o Ábaco
Se o aluno do EFI só consegue fazer abstrações pseudoempíricas, isso quer dizer que ele necessita do concreto para abstrair, fazer relações mentais.
Daí, professora, a importância do uso do ábaco para o ensino das contas de dividir.
O ábaco é um instrumento milenar, criado por volta de três milênios antes de Cristo.
Foi um artifício utilizado por inúmeros povos, babilônios, chineses, hindus, egípcios, gregos, romanos, árabes etc. para efetuar cálculos.
O ábaco possibilita operar quantidades: quando, por exemplo, professora, somo três argolas com mais quatro argolas, estou manipulando quantidades, 3 argolas mais 4 argolas.
Contudo, estou manipulando objetos, argolas, e atribuindo quantidades a essas argolas 3 e 4. Estou fazendo uma abstração pseudoempírica.
Dividir é desagrupar. Distribuo quantidades em partes iguais.
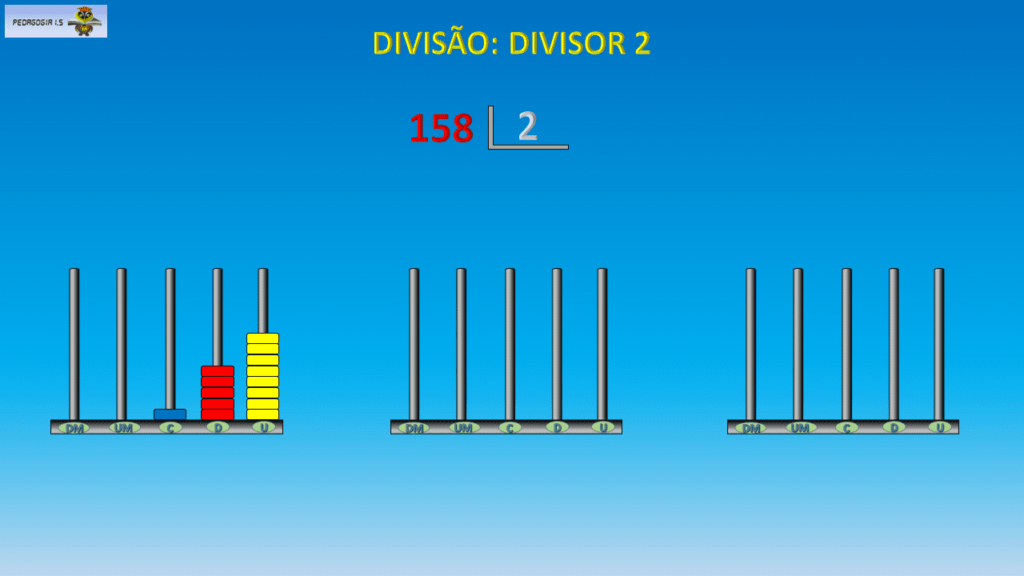
Para usar o ábaco na divisão, professora, por exemplo, 1443 ÷ 12, eu vou usar 12 ábacos para distribuir 1443. Isso pode ser visto neste vídeo.
O aluno vê a materialização da divisão. Ele vai distribuindo as quantidades, nos 12 ábacos, até perceber que sobra uma unidade que é o resto.
O Segredo Não Revelado das Contas de Divisão
Só por volta do século sexto depois de Cristo, os hindus criaram um sistema com dez símbolos, incluindo o zero, e depois os árabes o desenvolveram e divulgaram pela Europa, por isso são chamados indo-arábicos.
Os árabes perceberam a facilidade de operar esse Sistema de Numeração Decimal (SND) que facilitavam o processo de calcular.
Note, professora, que para chegar nas contas com os números, a humanidade levou milênios, pois seus fundamentos são o SND.
A conta de divisão é a mais difícil. Ela depende da aprendizagem das outras três operações: soma, subtração e multiplicação.
As defasagens nessas operações se acumulam e dificultam a operacionalidade do algoritmo, a conta, de divisão, professora.
E, mais fundamental, as contas são uma técnica. A manipulação de símbolos matemáticos, não de quantidades.
O algoritmo, a conta, professora é um passo a passo, uma receita técnica para operar os algarismos do Sistema de Numeração Decimal (SND).
Sua eficiência e eficácia são bastante evidentes: se você dominar a técnica, você não errará a conta, basta seguir fielmente o passo a passo para acertar.
Essa técnica, porém, apesar de sua eficiência e eficácia, e aparentemente simplicidade, é altamente complexa e sofisticada.
E, além de tudo, essa técnica é uma abstração refletida. Evidentemente, os alunos do 4º e 5º anos do Ensino Fundamental I, que estão no período das operações concretas e fazem abstrações pseudoempíricas, não conseguem se apropriar inteiramente da técnica.
Ou seja, seus cérebros ainda não se desenvolveram o suficiente, não atingiram ainda o período das operações formais.
Aí está o segredo dos erros nas contas, principalmente, as de divisão.
Porém, professora, há outro segredo excelente: essas dificuldades podem ser superadas de maneira fácil, basta usar o material concreto, no caso, o ábaco.
Como Superar de Modo Mais Fácil Esses Erros?
Você, professora, de certa maneira já trilha o caminho que leva a superar com facilidade esse erro, pois você chegou até aqui na leitura desse texto. Por quê?
Porque, como professora antenada, pesquisadora, ciente de sua formação como Cientista da Educação, pois, sendo a Pedagogia a Ciência da Educação, você é uma cientista, e sua sala de aula, o seu laboratório.
Você trilha o caminho do acerto já que faz Pedagogiação. Ou seja, uma ação pedagógica intencional, consciente, nas suas buscas, pesquisas, de atividades para melhorar seu processo de ensino-aprendizagem.
No entanto, professora, se sua ação pedagógica é consciente e intencional falta-lhe algo. O quê?
Ela está sendo uma Pedagogiação inorgânica. Por isso, propomos uma Pedagogiação1.5: uma ação pedagógica intencional, consciente, porém, orgânica e cientificamente orientada.
Orgânica pressupõe um caminho determinado, um todo coerente e organizado de forma a cumprir objetivos cientificamente orientados.
Como ferramenta de trabalho, a Pedagogiação1.5 segue a orientação de quatro ramos científicos:
● Semiótica: os números são símbolos e a Semiótica sendo a ciência que estuda os símbolos, os signos, facilita entender a forma como os símbolos atuam na Matemática;
● Psicanálise: os erros nas contas de divisão podem ter também a Ansiedade Matemática como um de seus componentes. Essa ansiedade dificulta a operacionalização da conta.
Utilizando como estratégia de ensino a Educação Narrativa, os preceitos psicanalíticos ajudarão você, professora, a superar os traços da Ansiedade Matemática;
● Psicogenética: o entendimento do período das operações concretas e que o aluno desse período faz abstrações pseudoempíricas são um forte aliado para ajudar você, professora, a eliminar o erro nas contas, principalmente, porque entende a necessidade de usar o ábaco (material concreto);
● Neurociência Cognitiva: saber que seu aluno, no período das operações concretas, erra por não ter ainda desenvolvido completamente seu cérebro facilitará muito seu processo de pesquisa.
Você, professora, terá uma atalho, pois, organicamente, intencionalmente, buscará atividades cientificamente orientadas que auxiliarão você e seus alunos a superarem os erros nas contas de dividir.
A Pedagogiação1.5 surgiu do LAPAPIEF – Laboratório de Pesquisa para Ação Pedagógica Interdisciplinar no Ensino Fundamental – um Laboratório de Iniciação Científica que por mais de 10 anos trabalhou com alunas e alunos de Pedagogia.
Desse Laboratório de Iniciação Científica, surgiu um método INOVADOR, ÚNICO, REVOLUCIONÁRIO a Pedagogia1.5.
A Pedagogia1.5 se apoia em cinco pilares fundamentais:
1. Educação Narrativa: tendo por base a História da Matemática e ideias da Psicanálise para ajudar a diminuir a Ansiedade Matemática de alunos.
2. Agrupamento: a História da Matemática nos mostra ser o Agrupamento o fundamento da Matemática.
3. Valor Posicional: aliado ao agrupamento o Valor Posicional, ou seja, o lugar que o algarismo ocupa no número, ajuda o aluno a perceber, a compreender, a razão dos algarismos 3 não terem o mesmo valor no número 33, por exemplo.
4. Sistema de Numeração Decimal: tanto o Agrupamento quanto o Valor Posicional estruturam o Sistema de Numeração Decimal (SND) e seu desconhecimento é o responsável direto pelos muitos erros estudantis.
5. Material Concreto: o uso do material concreto é uma necessidade a partir do conhecimento trazido pela Psicogenética e Neurociência Cognitiva já que o aluno do Ensino Fundamental I faz abstrações pseudoempíricas.
Entre os materiais concretos sugeridos e trabalhados pela Pedagogia1.5 estão os vídeos, além do ábaco e do material dourado. A Pedagogia1.5 utiliza Vídeos-oficinas prontos para serem utilizados em sala de aula com seus alunos, professora.
Você, pode ter essa experiência comprovada pegando uma amostra totalmente GRATUITA da Pedagogia1.5 e de sua sensacional ferramenta principal a Pedagogiação1.5 no Minicurso GRATUITO Pedagogia1.5.
Referências
PIAGET, Jean. Abstração reflexionante: relações lógico-aritméticas e ordem das relações espaciais. Porto Alegre: Artes Médicas, 1995.