FORMA POUCO CONVENCIONAL DE ENSINAR DIVISÃO EVITA ERROS DE ALUNOS DO 4º E 5º ANOS DO ENSINO FUNDAMENTAL I
As contas de dividir são o maior pesadelo de alunos e professores do 4º e 5º anos do Ensino Fundamental I.
O edifício da Matemática, como fala Piaget, se constrói pouco a pouco. A divisão é o ponto alto da construção.
Para que o aluno não erre o algoritmo de dividir, ele precisa saber muito bem as outras contas: somar, subtrair e multiplicar.
E isso não acontece. Os erros nas outras três operações matemáticas fundamentais, mostram as pesquisas, são menores na soma, aumentam na subtração e depois na multiplicação.
Se os alunos não dominam bem as três primeiras, é natural que esse acúmulo de erros impossibilite que os alunos operem bem a conta de dividir.
Por que esses erros são recorrentes em todas essas operações? Os alunos são burros? Ou você, professora, não sabe ensinar?
Este artigo, professora, vai explicar que não é nem burrice nem incompetência de sua parte.
Saber as razões que levam a esse acúmulo de erros vai libertar você da culpa de não saber ensinar e de uma possível estupidez do alunado.
Há um erro, sim, no sistema de ensino. A forma tradicional de ensinar as operações matemáticas fundamentais sempre esteve presa à técnica do algoritmo, ou seja, à técnica de fazer contas de maneira tradicional desde que os árabes a divulgaram pela Europa a partir do século XVI.
O Segredo Escondido Que Fará Você Compreender o Erro no Sistema de Ensino das Operações Matemáticas Fundamentais
O sistema de ensino da Matemática está preso a uma técnica secular que é muito eficiente e eficaz.
Caso você aprenda a técnica do algoritmo, a técnica das contas de somar, subtrair, multiplicar e dividir, você não errará nenhuma conta.
Porém, o sistema de ensino não levou em conta os avanços científicos, tanto psicogenéticos quanto neurológicos, que explicam o desenvolvimento da criança.
Há várias décadas, já se conhecem os períodos de desenvolvimento da criança. E o aluno do 4º e 5º anos do Ensino Fundamental I se encontra no período das operações concretas como comprovou teórica e praticamente os estudos piagetianos.
Isso explica as razões dos inúmeros erros cometidos pelos alunos.
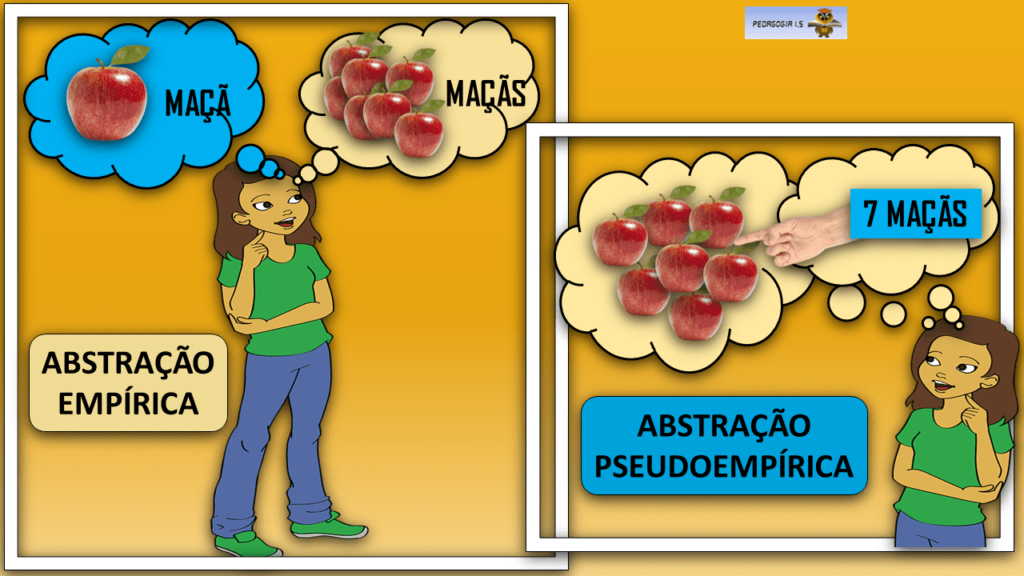
No período das operações concretas, os alunos PRECISAM de materiais concretos para que possam operar melhor, pois nesse período eles fazem abstrações pseudoempíricas.
O que isso quer dizer? Quer dizer que nessa faixa etária a criança só consegue pensar melhor, isto é, abstrair, quando se apoia em objetos concretos.
Quando vejo uma maçã, por exemplo, entre milhares de objetos à minha volta, eu reconheço esse objeto maçã e isso é fazer uma abstração empírica.
Reconhecer é trazer da memória um conhecimento. Aprendi que aquele objeto vermelho, no formato próximo de uma esfera, é uma maçã.
Conhecer é construir uma classificação mental do objeto, isto é, fazer uma abstração empírica, tirando dos objetos características que me ensinam o que aquele objeto é.
O que observo, o que experimento, me ensina sobre os objetos e ações. E quando tiro dos objetos suas características para conhecer esse objeto estou mentalmente construindo um conhecimento: estou fazendo uma abstração empírica.
No período das operações concretas, o desenvolvimento mental da criança já possibilita que ela faça abstrações mais elaboradas.
No entanto, ela não consegue fugir do concreto. Para pensar melhor, ela precisa se apoiar no objeto, por isso sua abstração é pseudoempírica.
Ao ver um grupo de maçãs, reconheço que são várias maçãs. Isso é um dado da realidade, empírico.
Se eu sei contar, e aponto com o dedo uma a uma das maçãs, estou atribuindo uma quantidade a cada maçã.
Conto sete maçãs. Sete é um símbolo matemático. Esse número é uma relação mental que fiz entre várias maçãs. Estou fazendo uma abstração pseudoempírica.
Ou seja, é uma abstração falsamente empírica porque, na realidade, eu crio relações numéricas mentais e coloco nos objetos agrupados maçãs.
Agora, se apresento ao aluno um problema aritmético para dividir 63 maçãs entre 8 alunos estou trabalhando com números, símbolos, e não com quantidades.
Ora, se o aluno do 4º e 5º anos do Ensino Fundamental I está no período das operações concretas ele sente grande dificuldade em operar apenas com números, pois é uma operação mental, abstrata.
Ele precisa se apoiar no concreto para conseguir operar de forma mais eficiente.
O segredo para abolir os erros nos algoritmos de divisão ou contas de divisão, erros do sistema de ensino tradicional, é você, professora, usar material concreto.
A Prova De Que os Alunos do Período das Operações Concretas Precisam Usar Material Concreto Tem Mais Uma Confirmação Científica
Durante décadas foram efetuados estudos e pesquisas sobre o período das operações concretas e inumeráveis livros e pesquisas confirmaram a teoria e prática (clínica) piagetianas.
Estudos científicos de outra área independente, a respeito do desenvolvimento do cérebro humano, vêm confirmando os estudos piagetianos.
O desenvolvimento do cérebro humano começa no embrião e prossegue na criança, no adolescente, terminando somente ao final da segunda década do adulto, ensina a Neurociência Cognitiva.
O estudo dos neurônios, células básicas do cérebro e do sistema nervoso, explica esse desenvolvimento cerebral, conforme pesquisas intensivas feitas pela Neurociência Cognitiva.
Por isso, o cérebro do aluno do Ensino Fundamental I não consegue processar bem as quatro operações matemáticas fundamentais.
Seu desenvolvimento cerebral, ainda imaturo, encontra enorme dificuldade em operar as contas de divisão.
As contas são uma técnica altamente abstrata e complexa. Ora, se o cérebro do aluno ainda é imaturo e, se ele predominantemente faz abstrações pseudoempíricas, como ele vai conseguir fazer uma operação que necessita de abstrações refletidas?
As contas, os algoritmos, por serem uma técnica, funcionam como uma receita, porém, abstrata: se seguirmos seus passos abstratos, conseguimos efetuar qualquer uma delas e não errar.
No entanto, para isso, professora, o aluno precisa do pensamento formal, próprio do período das operações formais, em que o cérebro já conseguiu uma maior maturidade biológica.
Se você, professora, quer que seu aluno não erre mais as contas de dividir, precisa usar o material concreto.
A Melhor Forma de Ensinar a Divisão É Utilizando o Material Concreto
Dentre os materiais concretos, o material dourado, criado por Maria Montessori entre o final do séc. XIX e início do séc. XX, torna-se um grande auxiliar no ensino das contas de divisão.
Montessori utilizou o material dourado com crianças deficientes mentais e elas aprenderam a operar contas tão bem que concorriam em nível de igualdade com as crianças não deficientes.
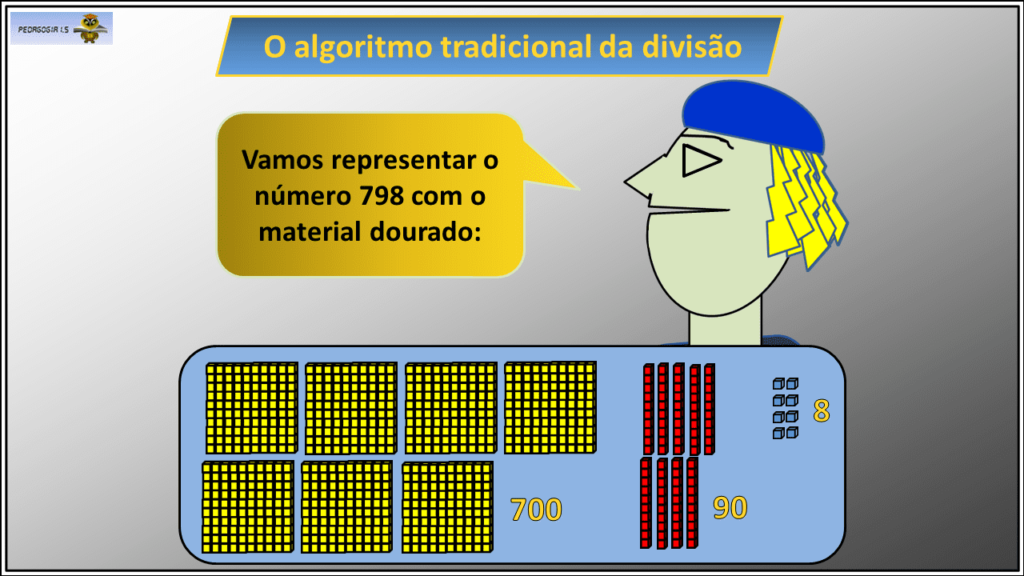
Ele é um material concreto estruturado, isto é, tem uma estrutura fundamentada no Sistema de Numeração Decimal (SND): os cubinhos representam as unidades, as barras, as dezenas, as placas as centenas e o cubão, a unidade de milhar.
Se dividir é repartir, desagrupar, concretamente, o aluno do Ensino Fundamental I vai operar com quantidades de cubinhos, barras e placas que representam os números.
Com isso, eles conseguem visualizar os números, concretamente, ao manipular as quantidades expressas nas peças do material dourado.
Ou seja, ele vai fazer abstração pseudoempírica, mas terá o apoio do concreto, para conseguir elaborar seu pensamento aritmético que deixa, por isso mesmo, de ser tão abstrato.
Ele vai visualizando, ao atribuir valores às peças e consegue entender o Valor Posicional próprio do SND.
O Valor Posicional fica explícito para ele, professora, principalmente nas trocas, quando precisa agrupar e desagrupar no “vai um”.
Consegue visualizar o “vai um” quando troca dez unidades por uma dezena ou dez dezenas por uma centena.
As operações com reserva trazem grande dificuldade para os alunos por serem eminentemente abstratas.
Transforme Sua Pedagogiação: Sua Ação Pedagógica Consciente e Intencional
Se você, professora, chegou a este artigo, isso é uma prova que faz Pedagogiação. Está pesquisando atividades matemáticas para aprimorar sua pedagogiação de forma consciente e intencional.
Age pedagogicamente como Cientista da Educação. Relembrando: Pedagogia é a Ciência da Educação, então você é uma Cientista Educacional.
Se usar o material dourado em sala de aula, vai transformar sua ação pedagógica para além do consciente e intencional e pode fazer isso de uma forma cientificamente orientada se usar como ferramenta a Pedagogiação1.5.
Essa ferramenta de trabalho, a Pedagogiação1.5 adota a bússola de quatro ramos científicos.
● Semiótica: sendo os números símbolos e a Semiótica, a ciência que estuda os símbolos, os signos, facilita perceber a maneira como os símbolos agem na Matemática;
● Psicanálise: os inúmeros erros nas contas de divisão podem decorrer, também, da Ansiedade Matemática. Essa ansiedade dificulta a operacionalização da conta.
Empregando como tática de ensino a Educação Narrativa, as ideias psicanalíticas auxiliarão você, professora, a suplantar os traços da Ansiedade Matemática;
● Psicogenética: a compreensão do período das operações concretas e de que a criança desse período faz abstrações pseudoempíricas é uma intensa aliada para auxiliar você, professora, a abolir o erro nas contas, sobretudo, porque percebe a necessidade de usar o material dourado (material concreto);
● Neurociência Cognitiva: entender que seu educando, no período das operações concretas, comete erros por não estar ainda com seu cérebro desenvolvido completamente vai facilitar bem seu processo de pesquisa.
Você, professora, vai ter um atalho, pois, intencionalmente, organicamente, vai procurar atividades cientificamente orientadas que ajudarão você e seus alunos a sobrepujarem os erros nas contas de dividir.
A Pedagogiação1.5 nasceu do LAPAPIEF – Laboratório de Pesquisa para Ação Pedagógica Interdisciplinar no Ensino Fundamental – um Laboratório de Iniciação Científica que, por mais de uma década, pesquisou com alunas e alunos de Pedagogia.
Desse Laboratório de Iniciação Científica, brotou um método ÚNICO, INOVADOR, REVOLUCIONÁRIO: a Pedagogia1.5.
A Pedagogia1.5 se ampara em cinco pilares básicos:
1. Educação Narrativa: tendo por apoio a História da Matemática e preceitos da Psicanálise para auxiliar a atenuar a Ansiedade Matemática de alunos.
2. Agrupamento: a História da Matemática nos ensina que o Agrupamento é o fundamento da Matemática.
3. Valor Posicional: junto do agrupamento, o Valor Posicional, isto é, a posição que o algarismo fica no número, auxilia à compreensão do aluno, à notar o porquê do algarismo 3 não ter o mesmo valor no número 33, por exemplo.
4. Sistema de Numeração Decimal: tanto o Valor Posicional quanto o Agrupamento estruturam o Sistema de Numeração Decimal (SND) e o desconhecimento deste é um dos culpados diretos pelos diversos erros estudantis.
5. Material Concreto: a utilização do material concreto é um imperativo a partir da informação trazida pela Psicogenética e Neurociência Cognitiva, pois o aluno do Ensino Fundamental I faz predominantemente abstrações pseudoempíricas.
Entre os materiais concretos indicados e trabalhados pela Pedagogia1.5 estão os vídeos, o ábaco e o material dourado. A Pedagogia1.5 emprega Vídeos-oficinas prontos para serem empregados na sua classe com seus alunos, professora.
Você, pode conseguir comprovadamente essa experiência, professora, adquirindo uma amostra completamente GRATUITA da Pedagogia1.5 e de sua esplêndida ferramenta capital a Pedagogiação1.5 no Minicurso GRATUITO Pedagogia1.5.
Referências
PIAGET, J.; SZEMINSKA, A. A gênese do número na criança. Rio de Janeiro: Zahar, 1981.