
O QUE É ENSINO ORGÂNICO: 11 MOTIVOS PARA VOCÊ USÁ-LO NAS ATIVIDADES MATEMÁTICAS DO ENSINO FUNDAMENTAL 1
Ensino Orgânico é uma ação didática cientificamente orientada, em que a professora age de modo consciente e intencional e se torna mediadora do processo ensino-aprendizagem e sabe exatamente quais atividades matemáticas trabalhar com seus alunos.
1. Qual a Importância do Orgânico para o Ensino de Atividades Matemáticas?
Você, professora, estudou e ensina o corpo humano para seus alunos.
Organismo é algum corpo composto por órgãos que interagem fisiologicamente e executam diferentes processos indispensáveis à vida.
Interação é a palavra a se destacar. Ação entre órgãos compõem o organismo.
Cada órgão exerce sua função: o estômago digere os alimentos; os pulmões filtram o ar que entra no organismo; tudo isso sob o comando do cérebro, do sistema nervoso.
Para as atividades do dia a dia, precisamos de energia. Por isso, nos alimentamos. Os alimentos são digeridos pelo estômago.
Nosso organismo pode ser comparado a uma fábrica. Ele trabalha incansavelmente 24 horas por dia. Responsabiliza-se por fazer e refazer os materiais que nossas células necessitam.
Para qualquer atividade que fazemos, precisamos de um combustível, de energia. Nosso organismo fabrica esse combustível que vem dos alimentos que ingerimos.
O carro só funciona se tiver combustível: gasolina ou álcool. O álcool ou a gasolina entra em combustão com o oxigênio do ar para gerar a energia.
No nosso organismo, os alimentos que consumimos reagem ao oxigênio para produzir à energia que precisamos.
Você já sabe disso tudo, professora. Só estamos relembrando para vermos a importância do orgânico para o ensino.
Os órgãos são individuais, porém, trabalham em sintonia uns com os outros. Essa interação é fundamental. Cada um exerce sua função em benefício dos demais.
Se um órgão se danifica, se fica doente, todo o organismo se ressente. Se algum deles parar completamente, ocorre a morte de todo o organismo. É a ausência da vida que se esvai.
Quer saber como o orgânico estrutura o ensino das atividades de matemática? Continue lendo e confira os próximos tópicos.
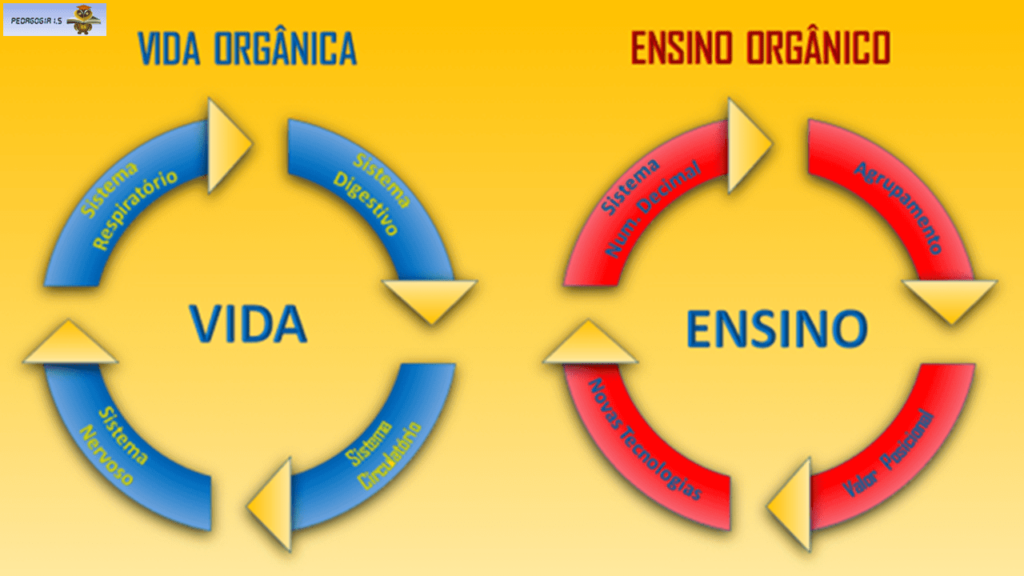
Na vida orgânica, o oxigênio e os nutrientes são distribuídos para todo o organismo, para cada célula, pelo Sistema Circulatório, sob o comando do Sistema Nervoso.
O ato de respirar é vital. Faz as trocas gasosas entre o meio ambiente e o corpo humano.
No Ensino Orgânico, o ato pedagógico, também, é vital. Faz as trocas didáticas entre o ensino e a aprendizagem.
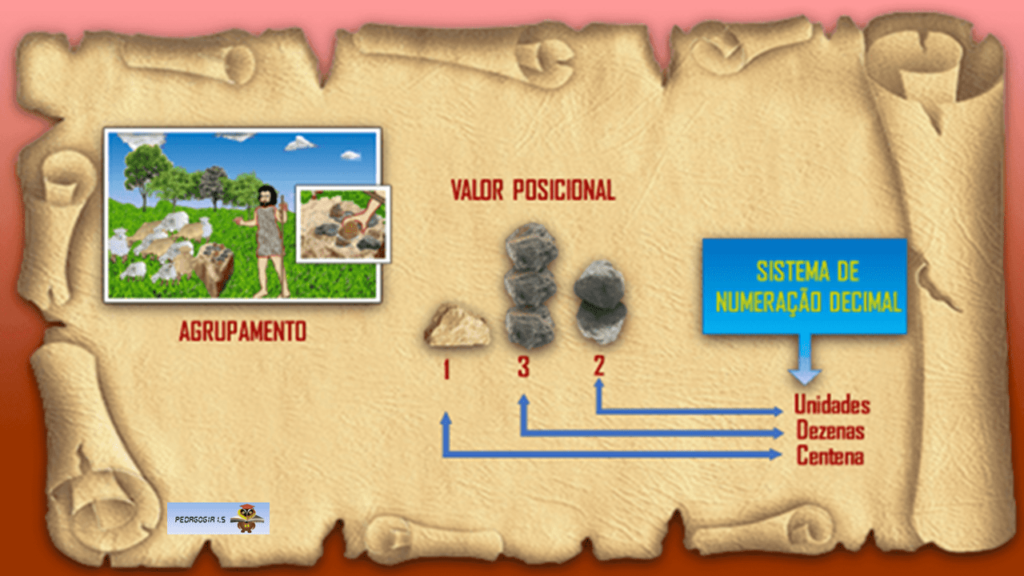
O Ensino Orgânico se estabelece a partir do Agrupamento, Valor Posicional e Sistema de Numeração Decimal. O meio de comunicação desse sistema se ancora nas Novas Tecnologias, principalmente, o vídeo e a História da Matemática.
2. Saiba Exatamente a Razão de Seus Alunos Fracassarem nas Atividades Matemáticas: É o Ensino Inorgânico
Em cursos de capacitação de professores, costuma-se contar a história de uma pessoa que ficou em coma por 30 anos.
Ao acordar, encontrou grandes dificuldades em conviver no cotidiano. Um novo palavreado e novas formas de comunicação a deixava perplexa.
Sendo da geração pré-internet, um novo vocabulário era incompreensível para ela: delete, mande um e-mail, procura no google, mande um SMS, post no Face ou no Insta etc.
Celulares com funcionalidades que ele não conseguia entender: sentiu-se um grande analfabeto. Então, resolveu voltar para a escola, para aprender.
Ao chegar na escola, sentiu-se muito confortável. Ali estava o lugar que conhecia: nada havia mudado nesses trinta anos.
As fotos abaixo exemplificam essa realidade:

Em essência, desde 1948, a primeira foto, mostra uma sala de aula em 1948, o século passado. A segunda, apresenta uma escola deste século.
Tudo igual: alunos sentados em frente a professora; a mesma lousa; a professora ensinando.
A mesma arquitetura, o mesmo sistema de ensino, embora tenham decorridos 74 anos.
E o ensino mudou? Não, continua o mesmo ensino inorgânico.
Inorgânico, como? Conteúdos dispersos, desconexos, fragmentados.
A principal caraterística do Ensino Orgânico é sua organização. Para ser orgânico, fazer parte de um organismo, precisa ser organizado: órgãos interdependentes.
Atividades matemáticas dispersas, xerocópias para alunos ocuparem seu tempo, se não forem previamente pensadas, encadeadas, são apenas uma forma de ocupar o tempo do aluno.
Quer entender melhor o que é Ensino Orgânico e a forma como ele pode ser a peça que estava faltando para que sua atividade de matemática funcione? Então, este artigo é para você!
3. Ciência: a Ferramenta Surpreendente Que Vai Alavancar Seu Estudo.
Se você, professora, pensou: Xii… Ciência é difícil. Pense e vamos relembrar: você é uma CIENTISTA DA EDUCAÇÃO.
Se Pedagogia, é a Ciência da Educação, então, obviamente, você é uma cientista da educação.
Você passou alguns anos em uma Faculdade de Pedagogia aprendendo diversas teorias para usar em um laboratório: a sua sala de aula.
A ciência, em um laboratório, faz experimentos. Alfabetizar, inclusive, matematicamente, é experimentar o tempo todo.
Se isso for feito de forma orgânica, organizada, consciente, intencionalmente, você vai orientar seu trabalho para o sucesso da aprendizagem.
Ciência pode ter um sentido mais amplo, também, como na frase: ter ciência de…
Ter ciência de é estar consciente de algo. Um Ensino Orgânico é estar ciente de um passo a passo a seguir no processo de ensino-aprendizagem.
Quando você elaborou seu TCC, Trabalho de Conclusão de Curso, você teve que lidar com ferramentas da produção científica. Duas nos interessa aqui: objetivos geral e específico.
No Ensino Orgânico, você, professora, precisa estar ciente de seus objetivos para que o ensino-aprendizagem de matemática seja efetivo.
Os objetivos organizam, tornam orgânico, seu trabalho.
Se seu objetivo geral for: Entender o que é agrupamento. Ao estabelecer seus objetivos específicos, professora, você especifica, torna explícito, organiza seus caminhos para o ensino e a aprendizagem de seus alunos.
Objetivos específicos para entender o que é agrupamento (sugestão, para exemplificar):
a) Agrupar materiais diferentes, para identificar o número de grupos possíveis de serem formados e se existem elementos soltos.
b) Realizar trocas de peças de determinado grupo por outra peça que tenha o mesmo valor.
c) Utilizar o ensino agrupamento a fim de contar quantidades.
Note, professora, que ao especificar cada objetivo, você organiza seu processo de ensino-aprendizagem. Você planeja sua ação.
4. Os Segredos do Agrupamento Que Você, Professora, Precisa Ficar Atenta
O nome Sistema de Numeração Decimal (SND) já traz implícito o Ensino Orgânico:
♦ Decimal: já é em si o agrupamento. A base 10 (decimal) é a do sistema. A História da Matemática considera os 10 dedos das mãos a sua origem. Cada mão é um grupo de 5 dedos, e as duas mãos dois grupos 5 dedos.
♦ Numeração: no SND, o número é posicional. O algarismo muda de valor de acordo com seu lugar no número. Com os 10 algarismos se pode escrever qualquer número e se pode fazer qualquer operação.
♦ Sistema: o organismo vivo é um sistema integrado. O SND também é um sistema integrado tendo como base o agrupamento, o Valor Posicional do algarismo que se estruturou no tempo conforme a História da Matemática.
Na infância da humanidade, o ser humano não sabia contar. Desconhecia os números.
Mas quantificar, saber a quantidade de objetos, sempre foi uma necessidade. Porém, como avaliar uma quantidade sem saber contar?
Até a quantidade de quatro, funciona o senso numérico. A percepção dessa quantidade não necessita do artifício de contar.
Como o pastor de ovelhas contava a quantidade de ovelhas que tinha na época em que o ser humano deixou de ser nômade e se fixou em algum lugar?
Ele usava um expediente concreto: a correspondência um a um.
Comparava seu grupo de ovelhas com objetos concretos, a princípio os dedos das mãos.
Até 10 ovelhas, podia-se fazer a correspondência um a um: uma ovelha para cada dedo da mão.
Porém, quando a quantidade de ovelhas aumentava para além de 10 ainda restava o artifício de se usarem, também, os 10 dedos dos pés.
Para além de 20, passou-se a utilizar pedras. Para cada ovelha uma pedra. Se sobrassem pedras, faltavam ovelhas.
A base de contagem nasceu da fisiologia humana: base 10. O agrupamento dos dedos das mãos.
Depois, na correspondência um a um com as pedras, agrupavam-se pedras comparando-as com o grupo de ovelhas.
Mais tarde, professora, o ser humano abstraiu mais ainda. Grandes quantidades de ovelhas, grandes quantidades de pedras. Inventou-se símbolos para essa correspondência ainda um a um.
Traços em madeira, em argila, em ossos, correspondiam, para cada traço, uma ovelha. Ou, também, nós em cordas.
A História da Matemática demonstra que dos traços se evoluiu para a abstração dos números escritos.
Importante concluir que a base dez do SND surgiu da primeira máquina de calcular do ser humano que são as mãos.
5. A verdade É Que a Compreensão do Que É o Valor Posicional Alavanca a Aprendizagem das Contas, os Algoritmos
A Helena, a garotinha do vídeo, teve uma iluminação: percebeu a diferença entre o 12 e o 21. Sacou que os dois números são formados pelos mesmos dois algarismos: 1 e 2.
Ela se deu conta do Valor Posicional.
O Valor Posicional, professora, foi uma das grandes descobertas do ser humano que fez evoluir muito a Matemática.
Possibilitou uma enorme economia de tempo e processos no fazer matemático. Apenas 10 algarismos: com eles podemos escrever qualquer número e fazer qualquer operação matemática.
O Valor Posicional (VP) é uma raridade na História da Matemática. Apenas 4 povos trabalharam o VP, informa Ifrah.
A primeira vez que ele surgiu, professora, foi com os babilônios 2000 anos antes da era cristã. Depois, os matemáticos da China descobriram o VP pouco tempo antes de Cristo. Os Maias trabalharam o VP entre os séculos III e V depois de Cristo.
Por fim, os matemáticos da Índia o usaram mais ou menos no século V.
Apenas 10 dígitos, professora, e podemos representar qualquer número. Isso só acontece porque o número muda de valor conforme a posição que ocupa.
Um único dígito significa uma unidade; dois dígitos, por exemplo, 44, quer dizer que tenho um grupo de quatro dezenas mais um grupo de quatro unidades.
A maioria dos alunos erram as operações matemáticas por não entenderem esse processo, principalmente, nas contas com reservas, quando, erroneamente, dizemos “vai um”, já que na realidade vai uma dezena.
6. Uma Maneira 100% Garantida de Evitar Erros nas Atividades Matemáticas: o Sistema de Numeração Decimal (SND)
O encontro de duas culturas construiu a grande síntese que é o Sistema de Numeração Decimal.

A cultura hindu e a cultura árabe criaram juntas o sistema numérico que revolucionou a Matemática e possibilitou um grande salto no conhecimento matemático.
Os árabes, professora, ao entrarem em contado com a escrita numérica hindu e sua grande invenção, o zero, perceberam sua grande utilidade, eficácia e síntese.
Eles perceberam, os árabes, que os indianos haviam criado um sistema de numeração que aliavam o Valor Posicional e a base dez.
Assimilaram o sistema hindu e passaram a se utilizar dele e o divulgaram pelo Ocidente, por isso, o SND é conhecido como sistema indo-arábico.
O ensino-aprendizagem da Matemática só se sustenta se seu processo se assentar sobre três pilares: agrupamento, Valor Posicional e Sistema de Numeração Decimal.
Esses pilares representam o alicerce do ensino e da aprendizagem da Matemática.
O surgimento do SND permitiu o encontro das histórias da escrita numérica e do cálculo, possibilitando o desenvolvimento da Matemática, das ciências e das técnicas contemporâneas.
Torna-se básico que os alunos tragam bem consolidado o SND para que consigam manipular os números, entender quantidades para bem realizar cálculos.
Se a criança não consegue fundamentar os conhecimentos matemáticos, dificilmente vai avançar na aprendizagem de conteúdos mais difíceis, pois a aprendizagem matemática é cumulativa e o que não se aprende bem dificulta o prosseguimento da aprendizagem.
Ao assimilarem bem o SND, as crianças se tornam aptas a resolver qualquer operação matemática.
7. Descubra de Forma Prática e Simples Como a História da Matemática Pode Auxiliar o Ensino Orgânico
Os Parâmetros Curriculares Nacionais – Matemática recomendam usar como recurso didático a História da Matemática porque:
a. Mostra a Matemática como criação do ser humano.
b. Revela as necessidades e inquietações de diversas culturas, em distantes momentos da História.
c. Os conceitos matemáticos vistos historicamente mostram-se como veículos de informações de valores culturais.
d. Ajuda a resgatar a identidade cultural do próprio aluno.
e. “Em muitas situações, o recurso à História da Matemática pode esclarecer ideias matemáticas que estão sendo construídas pelo aluno,”
f. E “especialmente para dar respostas a alguns “porquês” e, desse modo, contribuir para a constituição de um olhar mais crítico sobre os objetos de conhecimento”. (PCN – Matemática, p. 34).
O aluno deixa de ver a Matemática como algo puramente abstrato. Percebe que é uma construção e que ele pode também construir seus processos matemáticos.
8. Por Que Algumas Professoras Estão Sempre no “QUASE Consegui Que Meus Alunos Acertassem as Contas?
A resposta é simples: a Pedagogiação inorgânica.
Sim, a professora que busca atividades de matemática no Pinterest, por exemplo, em que as atividades são muito boas, diversificadas, precisa atentar se sua ação didática é orgânica.
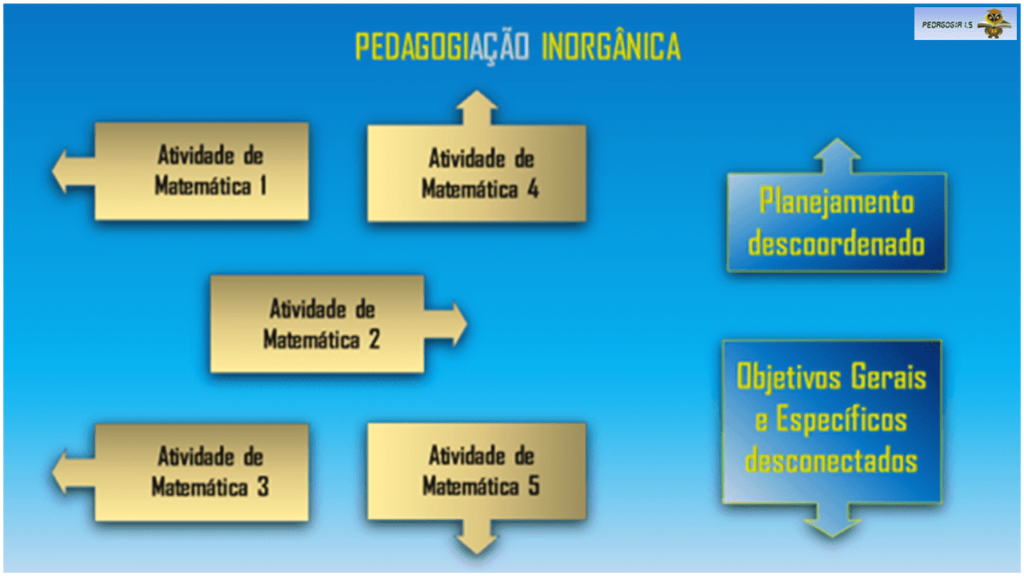
Por melhor que sejam as atividades elas precisam estar coordenadas entre si, ou seja, precisam ser organizadas, orgânicas.
Neste caso, há Pedagogiação, sim, embora seja uma ação pedagógica consciente e intencional, a consciência e a intencionalidade são superficiais.
Falta organicidade. Um saber fazer que seja como um passo a passo que conduza o processo de ensino-aprendizagem.
Por que os alunos fracassam nas contas? Exatamente por essa descoordenação geral.
O aluno, professora, assimilou o conteúdo das atividades conforme o que já sabe ou que considera fácil, de acordo com o esquema que já construiu. Não construiu um novo conhecimento.
Não conseguiu ir além daquele esquema que conhece. Ele sabe que se somar 3 + 3 + 3 + 3 = 12. O esquema que conhece é o da soma.
Mas falta-lhe a tomada de consciência, entender que 3 x 4 também é 12. Ele desenvolveria seu conhecimento acrescentando um novo elemento a seu esquema e perceberia uma nova forma, faria o que o pensamento piagetiano chama de acomodação.
Para que o aluno acomode, crie um novo esquema, o esquema de multiplicação, entender que somar 3 em 4 parcelas é igual a construir o conhecimento de que ele pode transformar as parcelas em um fator de 4.
O aluno atingiria um nível superior de tomada de consciência ele construiria o conceito de multiplicação.
O seu papel, professora, seria mediar o ensino e a aprendizagem. Ao coordenar os processos de ensino.
Para isso, seu ensino precisa ser orgânico.
Quer entender como isso pode ser feito? Continue a leitura e perceberá melhor o processo.
9. Finalmente, Uma Maneira Testada e Aprovada De Ensinar as Operações Matemáticas Sem Precisar se Preocupar Muito!
Essa maneira surgiu no LAPAPIEF – Laboratório de Pesquisa para Ação Pedagógica Interdisciplinar no Ensino Fundamental. Um laboratório de Iniciação Científica que trabalhou o ensino de matemática com alunas e alunos de Pedagogia.
É a Pedagogiação1.5: uma ação pedagógica cientificamente orientada em que as ações são conscientes, intencionais e orgânicas.
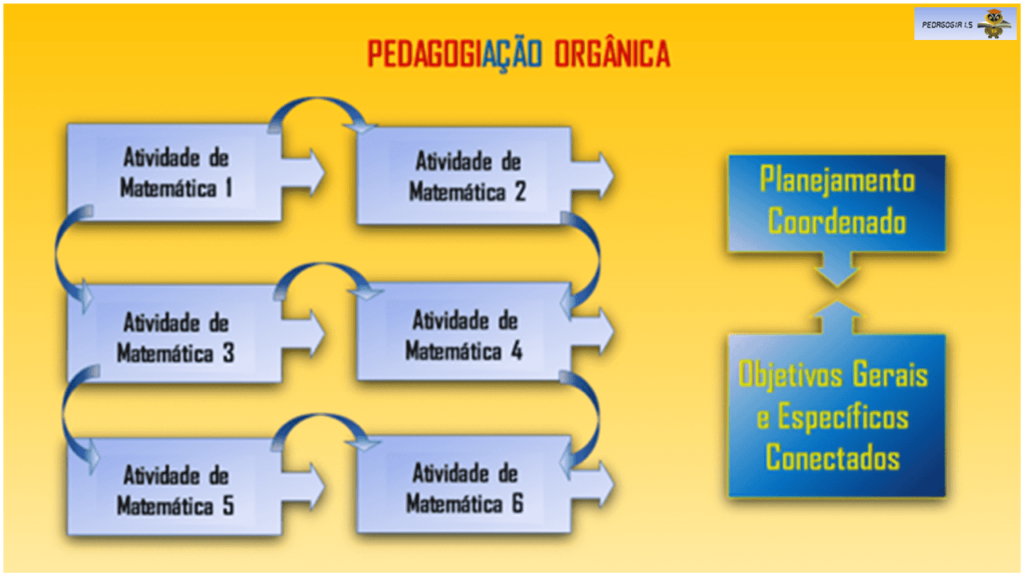
Uma ação pedagógica cientificamente orientada. O comando da ação fica por conta do saber científico que você aprendeu na faculdade, professora, já que é necessário, talvez, despertar a Cientista da Educação adormecida em você.
Intenção é a ação da mente anota Peirce. Usando o mercador das Mil e Uma Noite, Peirce mostra que ao jogar fora o caroço da tâmara ele feriu o olho do demônio.
Este foi um ato puramente mecânico, sem intencionalidade. Mas, se o mercador tivesse mirado o olho do demônio, teria havido uma intenção, uma mediação.
A Pedagogiação inorgânica ocorre de forma não intencional. A Pedagogiação Orgânica tem intencionalidade explícita, faz a mediação ensino-aprendizagem.
Planejamento escolar é algo chato. Mas planejar é essencial à vida humana. Você, professora, o utiliza quase inconscientemente no cotidiano.
Às vezes ele é rotina. Você planeja, professora, todos os passos que vai dar do levantar até chegar à escola. Na realidade, tudo foi planejado. Já imaginou se tudo fosse feito de improviso? Você não conseguiria realizar as tarefas mais simples.
Por que uma aula a ser ministrada seria diferente? Ela precisa ser planejada, organizada, orgânica.
Ter várias atividades para que os alunos façam, desconectadas, não significa organização, organicidade.
O que a Pedagogiação1.5 propõe é o orgânico: as atividades organizadas com objetivos especificamente orientados de forma científica para que a mediação ensino-aprendizagem ocorra de forma natural, porém orgânica.
Para isso, a proposta da Pedagogiação1.5 é a utilização, principalmente, de Vídeos-oficinas.
Veja, no próximo motivo, o porquê de usar os Vídeos-oficinas.
10. A Ferramenta Surpreendente: Vídeos-oficinas Como Novas Tecnologias no Ensino das Atividades Matemáticas
Ainda os Parâmetros Curriculares Nacionais – Matemática recomendam o recurso às Novas Tecnologias.
Costuma-se brincar no meio escolar a respeito da ‘didática do cuspe e do giz”.

A escola do passado assentava-se basicamente na lousa e no giz. Pierre Levy fala-nos, professora, das tecnologias da inteligência.
O giz e a lousa podem ser vistos como uma tecnologia da inteligência. Mas pode ser pensada como uma tecnologia perversa.
Tecnologia genial: simples, barata, fácil de usar. Basta um giz e uma lousa para que uma aula seja ministrada.
Mas perversa, se atentarmos, professora, que sua simplicidade e eficácia aprisionou a educação na ditadura do “cuspe e giz”.
Hoje, outra tecnologia da inteligência parece superar o giz. A xerocópia. De certa forma, a cópia xerográfica é o uso das novas tecnologias.
Porém, também pode se transformar, e para algumas escolas isso acontece, numa forma também perversa de uso, se não for utilizada de forma orgânica.
Os alunos do Ensino Fundamental e mesmo do Ensino Médio são da geração que nasceram com a Internet e o celular.
Uma geração alfabetizada naturalmente na linguagem do vídeo. Ela domina a gramática do vídeo. Nasceram e cresceram assistindo vídeos.
Como esta geração vai aceitar ser ensinada na didática do cuspe e giz? Ou mesmo da xerocópia. Esta precisa, no mínimo ter imagens e ter estética agradável.
A Pedagogiação1.5 enfatiza o uso dos vídeos em sala de aula. E a Pedagogia1.5 mostra como isso pode ser feito e facilitado. Veja no próximo item.
11. Como Você Se Sentiria Se Pudesse Ensinar Matemática Sem Ficar Horas Preparando Aulas
A Pedagogia1.5 nasceu do LAPAPIEF – Laboratório de Pesquisa para Ação Pedagógica Interdisciplinar no Ensino Fundamental.
Um laboratório de Iniciação Científica criado para trabalhar como ensinar matemática com alunas e alunos de Pedagogia. Veja mais sobre o LAPAPIEF aqui.
Quando foi criado o Laboratório de Iniciação Científica, imaginávamos que bastaria criar planos de aulas para resolver o problema do ensino de matemática.
O que os 10 anos do Laboratório demonstrou foi que planos de aulas são apenas um saber a ser ensinado. Ou seja, ele é o saber das apostilas, dos livros didáticos.
Existe um saber ensinado. O saber em ação na sala de aula. Quer dizer: o professor precisa transpor o saber do livro didático, da apostila e transformar esse saber a ser ensinado em saber ensinado.
Isto está bem explicado e trabalhado na Teoria da Transposição Didática de Yves Chevallard.
Como você, professora, que costuma ter jornadas de trabalho duplas, triplas ou maior teria tempo para transpor didaticamente o ensino a ser ensinado.
A Pedagogia1.5 oferece uma ferramenta incrível para você, professora, testar em sala de aula. Aperte o botão abaixo e baixe o Minicurso Pedagogia1.5 grátis.
São quatro Vídeos-oficinas Grátis, prontas para você trabalhar em sala de aula com seus alunos.
Uma boa Introdução à Matemática para você iniciar o ensino das Quatro Operações Matemáticas Fundamentais.
Se você gostar do Minicurso Pedagogia1.5 vai entender a razão de o Método Pedagogia1.5 ser ÚNICO, INOVADOR e REVOLUCIONÁRIO.
Com Vídeos-oficinas que irão liberar você, professora, do trabalho exaustivo de transpor didaticamente o ensino a ser ensinado (planos de aula, livros didáticos, apostilas).
São Vídeos-oficinas prontas para você usar em sala de aula para que seus alunos aprendam de vez As Quatro Operações Matemáticas Fundamentais e nunca mais errem as contas.
Descubra Como Ensinar as Quatro Operações Matemáticas Fundamentais e Ministrar Aulas Lúdicas Sem Precisar Perder Horas e Horas Preparando as Aulas. Veja agora mesmo.
Referências
CHEVALLARD, Yves. Sobre a teoria da transposição didática: algumas considerações introdutórias. In Revista de Educação, Ciências e Matemática, v.3, n.2, mai/ago, 2013. Disponível em: < http://publicacoes.unigranrio.edu.br/index.php/recm/article/view/2338/1111 >. Acesso em: 25 mar 2022.
LÉVY Pierre. As tecnologias da inteligência: O Futuro do Pensamento na Era da Informática, 2014. Disponível em: < https://lucianabicalho.files.wordpress.com/2014/02/as-tecnologias-da-inteligencia.pdf >. Acesso em: 22 mar 2022.
PEIRCE, Charles S. Semiótica. Editora Perspectiva: São Paulo, 1977.


