O SEGREDO PARA ENSINAR DE FORMA FÁCIL A MULTIPLICAÇÃO AO 3º ANO DO EF1: USAR O MATERIAL DOURADO
A multiplicação é uma das contas em que os alunos do 3º ano do Ensino Fundamental I mais erram. Descubra, professora, como você pode ensinar a multiplicação de uma maneira fácil e a razão dos alunos errarem tanto.
O material dourado facilita ensinar a multiplicação como soma de parcelas, também, a forma comprovada da aprendizagem do “vai um”.
Você, professora, tem um trabalho difícil e solitário: ensinar. E ensinar Matemática quase sempre é desesperante e desanimador. Provavelmente, você já sentiu, muitas vezes, a vontade de jogar a toalha…
No seu ofício de ensinar as contas de multiplicar, o algoritmo da multiplicação, quando vê a quantidade de erros e a aparente incapacidade de seus alunos de multiplicar você pode se sentir perdida inúmeras vezes.
O ensino da Matemática é cumulativo. Para efetuar bem a conta de multiplicar, as crianças precisam ter aprendido bem a adição e a subtração. Sem esses pré-requisitos é natural que os erros aconteçam.
Diante da História Matemática: Se uma caixa de lápis de cor tem 6 lápis, quantos lápis terão 3 caixas de lápis de cor como essa?
Se a criança ainda não aprendeu a multiplicar, ela pode resolver essa História Matemática? Claro que pode. Ela poderá recorrer à soma de parcelas e somar 6 + 6 + 6.
Por isso, para facilitar o ensino da conta de multiplicar, professora, provavelmente, você recorre à soma de parcelas iguais.
Pode parecer que isso facilita a compreensão do que é multiplicar. Parece evidente que 6 + 6 + 6 = a 3 x 6.
Contudo, a coisa não é assim tão simples, professora. A adição é uma operação natural. O próprio ato de contar, na realidade, é somar: você soma uma unidade ao número anterior ou ao seu antecessor.
A Matemática trabalha com símbolos. Tudo muito abstrato. O x é uma letra do alfabeto, aliás, uma das mais difíceis para o aluno aprender, uma vez que ele possui uma forma de escrita, mas pode ser lido e falado como z, s, chi…
Possivelmente, o aluno não guarda uma recordação muito boa do aprendizado dessa letra, se é que ainda não sente dificuldades em lidar com ela.
E, na Matemática, ganha uma simbologia completamente diferente: ele vai representar um sinal que significa multiplicar, no caso da operação de multiplicação.
Empatia, como você sabe, professora, é a capacidade de se colocar no lugar do outro. Pense na situação de seus alunos ante o desafio, complexamente abstrato, de entender a letra x, e ainda ter que associá-la e entendê-la como sinal multiplicativo.
Livre-se do Erro nas Contas de Multiplicação: Entenda o Segredo da Abstração
Disposição Quadrangular
Como adultos, que já construímos a noção de número, parece muito fácil perceber que a soma de parcelas é uma multiplicação. Mas isso não é evidente e fácil para o aluno.
As coisas vão se complicar mais ainda, professora, se tornando muito mais abstrata, quando é preciso calcular em uma organização retangular ou disposição quadrangular.
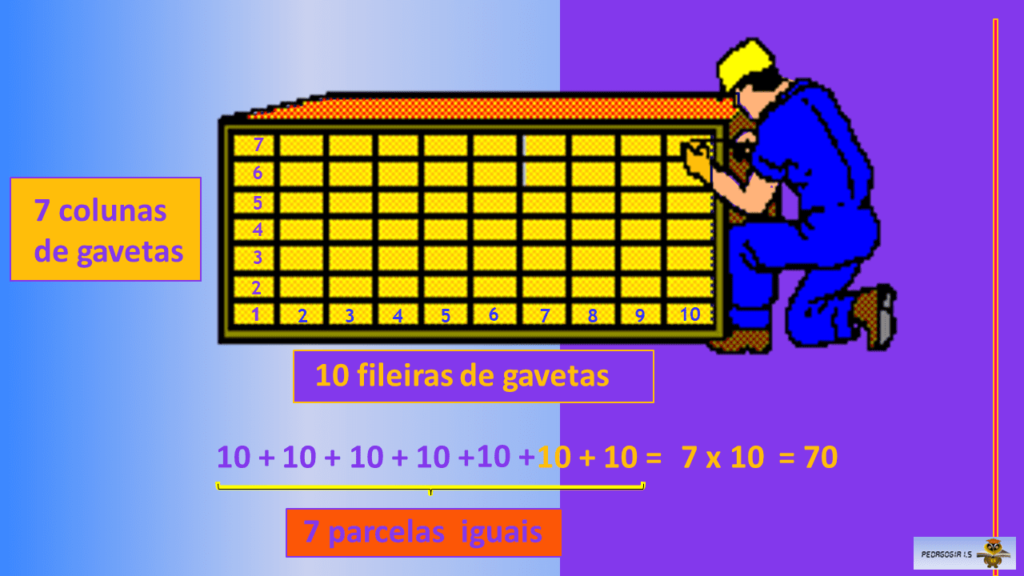
Pense na seguinte História Matemática: José, o marceneiro, construiu um gaveteiro para Joana, quantas gavetas tem o gaveteiro.
Você pode resolver essa História Matemática contando uma a uma as gavetas, porém, é um processo trabalhoso. Usar a multiplicação facilita o processo, pois basta contar as gavetas da primeira fileira e as da primeira coluna, depois é só multiplicar.
Uma complicação ainda mais gritante surge na multiplicação com reserva, o famoso “vai um”. Se já estava complicado, fica muito mais difícil. O reagrupamento é algo bastante abstrato que as crianças sentem muita dificuldade em compreender.
Você percebeu que a palavra abstrato apareceu inúmeras vezes neste texto, não é professora? Isso foi proposital.
Abstração é um processo mental. Vemos o mundo pela janela de nossos sentidos. O mundo está repleto de milhões de informações ao nosso redor. Não conseguimos e nem podemos prestar atenção em tudo.
Ao focarmos nossa atenção em determinada coisa, vemos, ouvimos, tocamos, cheiramos ou sentimos o gosto de determinado alimento. Nossos sentidos captam a informação que é processada em nosso cérebro.
A informação, ao ser processada em nosso cérebro, é uma abstração. Se olhamos para um objeto e o denominamos, uma maçã, essa denominação é uma abstração, retiramos daquele objeto determinadas informações, visuais, olfativas que nos fazem reconhecer aquele objeto.
Esse processo de reconhecimento de um objeto é o que a teoria piagetiana das abstrações chama de abstração empírica. Tiramos informações do objeto para reconhecer esse objeto.
Ao reconhecer uma bicicleta, também fazemos uma abstração empírica. Porém, se pensarmos bicicleta ecológica, o adjetivo ecológico acrescenta uma qualidade ao objeto bicicleta.
Qualidade que pusemos no objeto bicicleta. Isso é uma abstração pseudoempírica.
É um processo mental, uma relação que estabeleço com aquele objeto bicicleta.
E o número, professora? Ele não é um objeto. É um símbolo de uma quantidade. Contar é um processo abstrato. Atribuo uma quantidade a um ou vários objetos.
Agrupo objetos para contar esses objetos: uma maçã, duas maçãs, três maçãs etc.
Operação especificamente mental. Mesmo que a criança cante os números não quer dizer que ela já tenha adquirido a noção de número, que ela já tenha se apropriado da capacidade de atribuir um valor, uma quantidade, ao símbolo que é o número, diz Piaget.
A criança precisa de vários anos para construir a noção de número. E a conta, professora, é um processo ainda mais abstrato. A conta é uma técnica que levou milênios para ser construída pelo ser humano.
A conta, o algoritmo, é um passo a passo que usamos para efetuar, no caso, uma operação de multiplicação.
Para multiplicar 7 vezes 19, por exemplo, devemos escrever o 19, embaixo dele o 7, também embaixo do 9, um traço abaixo do 7 e colocamos do lado o x, que significa que a conta é de multiplicar.
Então, fazemos uma série de operações faladas e escritas: 7 vezes 9 igual a 63. Escrevemos o 3 embaixo da linha e do 7 e dizemos vai 6 e escrevemos o 6 acima do 1.
Depois dizemos, 7 vezes 1 é sete, mais 6 é igual a 13. Escrevemos, então, o 13 na frente do 3.
Observe, professora, que esse é um passo a passo infalível. Se fizermos esse passo a passo com qualquer número, fatalmente, se não cometermos algum equívoco, efetuaremos e acertaremos a conta.
É uma técnica, complexa, sofisticada e muito ABSTRATA. Na realidade, não estamos manipulando quantidades, mas, sim, manipulando símbolos, que também são abstratos.
Tudo isso é um processo abstrato em que se faz uma abstração reflexiva. A teoria das abstrações piagetianas são muito bem explicadas, de forma minuciosa, por Becker.
A Prova de Que no Período das Operações Concretas É Preciso Usar Material Concreto
Há décadas, um alerta já era dado a respeito da dificuldade do aluno do Ensino Fundamental I compreender esse processo, pois ele está no período das operações concretas.
Como você se lembra, professora, no período das operações concretas, ensinado pelos estudos piagetianos, a criança só consegue fazer operações abstratas apoiada no concreto. Nesse período ela faz abstrações pseudoempíricas.
Por isso, ela erra tanto as contas de multiplicar. As contas de multiplicar, muito abstratas, dependem de abstrações reflexivas.
O aluno do Ensino Fundamental I, ainda no período das operações concretas, não consegue fazer as contas ou faz isso com grande dificuldade, pois ele ainda não consegue fazer abstrações reflexivas que são próprias do período das operações formais a partir dos 11 a 12 anos.
Toda essa explicação foi também confirmada pela Neurociência Cognitiva.
A Neurociência Cognitiva estuda a forma como o cérebro opera. A maneira como os neurônios, as células que compõe o cérebro, e o sistema nervoso trabalham.
E explica que o aluno do Ensino Fundamental I ainda não desenvolveu seu cérebro o suficiente, pois o cérebro só completa seu desenvolvimento por volta do final dos vinte anos.
Isso mostra a impossibilidade biológica, do cérebro do aluno efetuar uma conta que é um processo abstrato que requer a abstração refletida enquanto ele só é capaz de fazer abstrações pseudoempíricas.
Por isso, a recomendação de trabalhar materiais concretos com o aluno do Ensino Fundamental I que está no período das operações concretas.
A recomendação é do próprio Piaget e a Neurociência Cognitiva veio comprovar, também, o acerto da sugestão piagetiana.
Contas de Multiplicar Sem Erros? É Fácil se Fizer Isso: Usar o Material Dourado
O material dourado é um material concreto estruturado. Foi criado e pensado por Maria Montessori, ao perceber que crianças deficientes aprendiam mais pela ação que pelo pensamento.
Montessori criou vários materiais pedagógicos, entre eles o material dourado. Foram desenvolvidos entre o final do século XIX e início do século XX. E os resultados tanto com crianças deficientes mentais e crianças não deficientes foram surpreendentes.
O material dourado é um material concreto estruturado pela razão de sua construção ter como fundamento a estrutura do Sistema de Numeração Decimal (SND): os cubinhos representando as unidades, as barras, as dezenas, as placas, as centenas.
O Sistema de Numeração Decimal é também um sistema altamente complexo e abstrato que se fundamenta no Agrupamento e Valor Posicional.
A dificuldade em entender o SND, pelos alunos, é uma das razões deles errarem tanto as contas. Para a criança do Ensino Fundamental I, com sua imaturidade biológica, o SND é muito abstrato e o material dourado facilita a sua compreensão.
Se você, professora, está lendo este artigo, provavelmente, chegou aqui através do Pinterest. Então, você já faz Pedagogiação, isto é, uma ação pedagógica consciente e intencional, pois está em busca da melhor forma de ensinar a Matemática.
Uma Ferramenta Surpreendente Que Desvelará o Segredo das Contas de Multiplicar Sem Erros

A primeira professora está em dúvida. A segunda professora, sugere o que fazer.
A Pedagogiação1.5 é ação pedagógica cientificamente orientada, atendendo a sua condição de Cientista da Educação: relembrando, professora, se a Pedagogia é a Ciência da Educação, você é, por consequência, uma Cientista da Educação.
A Pedagogiação1.5, estudando a Matemática, se apoia em quatro ciências:
● Semiótica: o número são símbolos que representam as quantidades e a Semiótica, ao estudar, os símbolos, os signos, ajuda a entender melhor esse processo.
● Psicanálise: os erros das contas em Matemática podem ocorrer, para além da imaturidade biológica dos alunos, em razão da Ansiedade Matemática, e utilizando como estratégia de ensino a Educação Narrativa, pode diminuir a Ansiedade Matemática.
● Psicogenética: os erros nas operações fundamentais matemáticas se devem, como apontou Piaget, ao fato do aluno do Ensino Fundamental I se encontrar no período das operações concretas e fazer abstrações pseudoempíricas. Esse entendimento auxiliará você, professora, a utilizar estratégias como o material dourado para reduzir esse problema.
● Neurociência Cognitiva: confirmou a teoria das abstrações piagetianas e nos ensina a imaturidade biológica do cérebro da criança do Ensino Fundamental I que, por se encontrar no período das operações concretas, precisa de material concreto para fazer abstrações.
A Pedagogiação1.5 é uma ferramenta da Pedagogia1.5, um método Inovador, Único, Revolucionário.
Surgiu de Oficinas Pedagógicas com alunas e alunos de Iniciação Científica de Pedagogia no LAPAPIEF – Laboratório de Pesquisa para Ação Pedagógica Interdisciplinar no Ensino Fundamental.
Esse Laboratório de Iniciação Científica ensinou, na prática e teoricamente, formas de melhor trabalhar o ensino de Matemática para uma aprendizagem mais consistente e eficaz.
Daí surgiram Vídeos-oficinas, prontos para serem utilizados por você, professora, em sala de aula com seus alunos e conseguir uma melhora surpreendente no seu ensino- aprendizagem.
Você, professora, pode ter uma amostra totalmente GRATUITA da Pedagogia1.5 e de sua ferramenta principal a Pedagogiação1.5 no Minicurso GRATUITO Pedagogia1.5.
Referências
BECKER, Fernando. Abstração pseudo-empírica e reflexionante: significado epistemológico e educacional. Shème: Revista Eletrônica de Psicologia e Epistemologia Genética, v. 6, Edição Especial, nov. 2014, p. 104-128. Disponível em: < http://www.bjis.unesp.br/revistas/index.php/scheme/article/view/4276/3105 >. Acesso em: 02 mar. 2023.
PIAGET, J.; SZEMINSKA, A. A gênese do número na criança. Rio de Janeiro: Zahar, 1981.
ZATTI, F.; AGRANIONIH, N. T.; ENRICONE, J. R. B. Aprendizagem matemática: desvendando dificuldades de cálculo dos alunos. In: PERSPECTIVA, Erechim. v.34, n.128, p. 115-132, dezembro/2010. Disponível em: < https://www.uricer.edu.br/site/pdfs/perspectiva/128_142.pdf >. Acesso em: 19 set. 2022.