APLIQUE ESSA TÉCNICA COM SEU ALUNO DO 3º ANO DO EF1 E ELE NÃO VAI MAIS ERRAR CONTAS DE MULTIPLICAR
Pode ser desesperador o seu dia a dia como profissional do ensino, professora, ao se deparar com os erros que seus alunos cometem nas contas de multiplicar.
Como você se sente, professora, ante esses erros? Às vezes você não tem vontade de desanimar? Sente que parece que você não sabe ensinar ou que seu aluno é burro.
Mas tenho um segredo pra te revelar, professora: não é que você não sabe ensinar e nem seu aluno é burro. Novas descobertas científicas vieram provar que o modo como ensinamos Matemática está errado.
É isso mesmo, professora. O sistema de ensinar a disciplina está equivocado. As teorias e pesquisas já vinham demonstrando esse problema. Porém, agora temos mais comprovações científicas de que o sistema está equivocado.
A Neurociência Cognitiva demonstra que o aluno, na faixa etária em que se encontra, alunos do Ensino Fundamental I, ainda estão desenvolvendo biologicamente seus cérebros.
O desenvolvimento cerebral do der humano só se completa por volta dos seus vinte anos finais.
Então, biologicamente, a criança do Ensino Fundamental I é imatura. Seu cérebro não consegue processar pensamentos abstratos como o faz o adulto.
O Segredo Por Trás do Período das Operações Concretas Que Você Desconhece
Você se lembra dos períodos de desenvolvimento que estudou no curso de Pedagogia, professora.
O período sensório motor, o pré-operacional, o das operações concretas e o das operações formais.
O estudo do período das operações concretas e o alerta piagetiano já diziam, teoricamente e em sua prática clínica, que a criança desse período para operar conteúdos abstratos precisa se apoiar no concreto.
Em cada período para operar conteúdos mentais, fazer, portanto, abstrações, o ser humano faz determinadas formas de abstrações:
Esse estudo da teoria das abstrações é facilitado pelo artigo de Becker.
Ao olharmos um objeto, por exemplo, uma bicicleta, a reconhecemos como bicicleta. Estamos fazendo uma abstração empírica. Esse conhecimento foi criado com nossa experiência: tiramos desse objeto as características que nos faz reconhecer a bicicleta.
Se pensamos, porém, bicicleta ecológica, atribuímos uma qualidade à bicicleta que colocamos nela, o ecológico. Isso é uma abstração pseudoempírica.
Quando pensamos em um número, estamos pensando em um símbolo que representa uma quantidade. Uma bicicleta, duas bicicletas. Estabelecemos uma quantidade para uma ou mais bicicletas. Isso é uma abstração reflexionante.
Quando o aluno consegue perceber que a soma de 3 + 3 + 3 = 3 vezes 3, ele faz uma abstração refletida. Ele reflete em cima de uma abstração reflexionante. Ele elabora um pensamento em cima de outro pensamento.
Toda essa teoria e prática foram também confirmadas pela Neurociência Cognitiva. Em cada período o ser humano só consegue operar de acordo com sua maturidade cerebral.
Cada abstração que ele faz, é feita conforme sua maturidade biológica permite.
Por isso, professora, o aluno do 3º ano do Ensino Fundamental I, estando no período das operações concretas, erra tanto as contas de multiplicar e as outras operações, também.
Ele faz abstrações pseudoempíricas, mas as contas, os algoritmos, são abstrações refletidas, próprias do período das operações formais.
Tudo Que Você Precisa Para Reverter Esse Processo É Usar Material Concreto: No Caso, o Ábaco
Se a teoria e práticas piagetianas já apontavam para a necessidade de usar o ábaco nesse período, agora, isso ganhou um respaldo maior com os estudos comprovando a imaturidade cerebral nesse período com a Neurociência Cognitiva.
No período das operações concretas, é preciso usar o ábaco. Essa é uma recomendação do próprio Piaget.

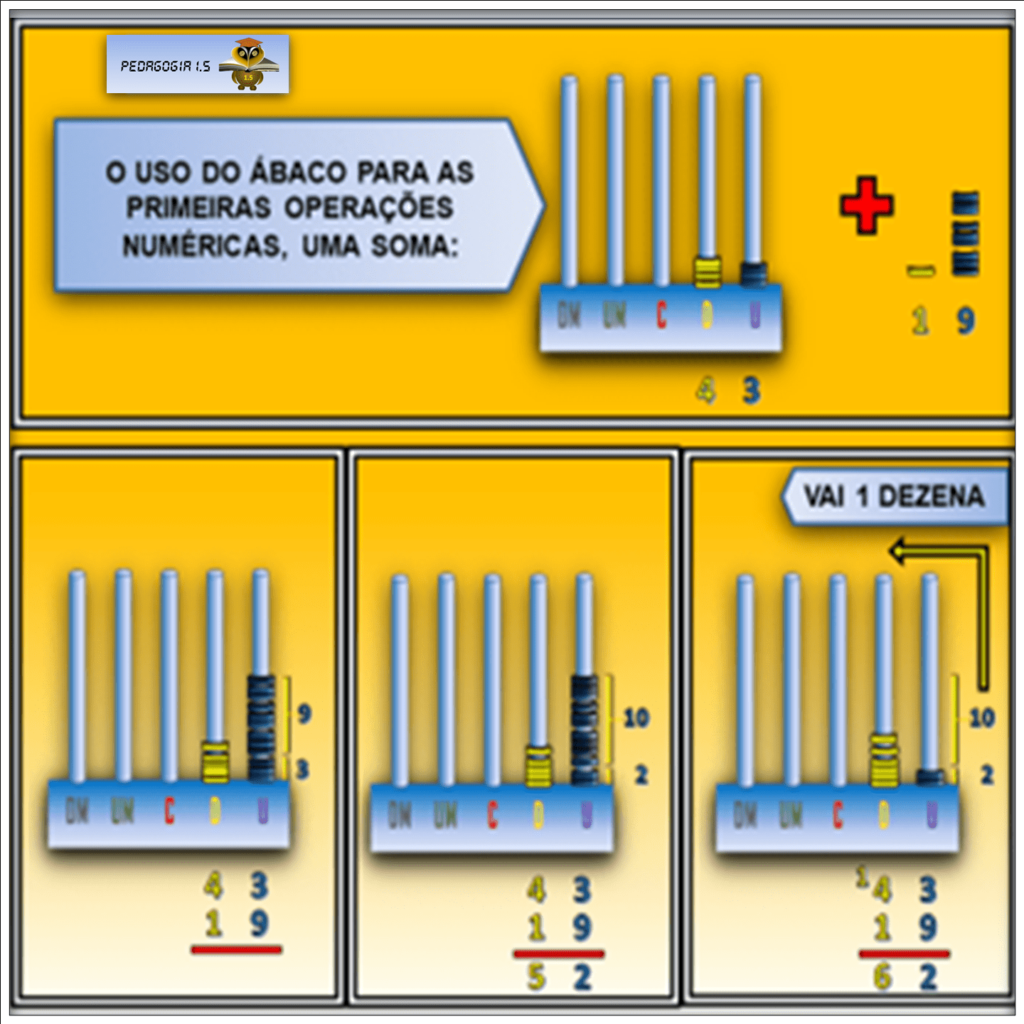
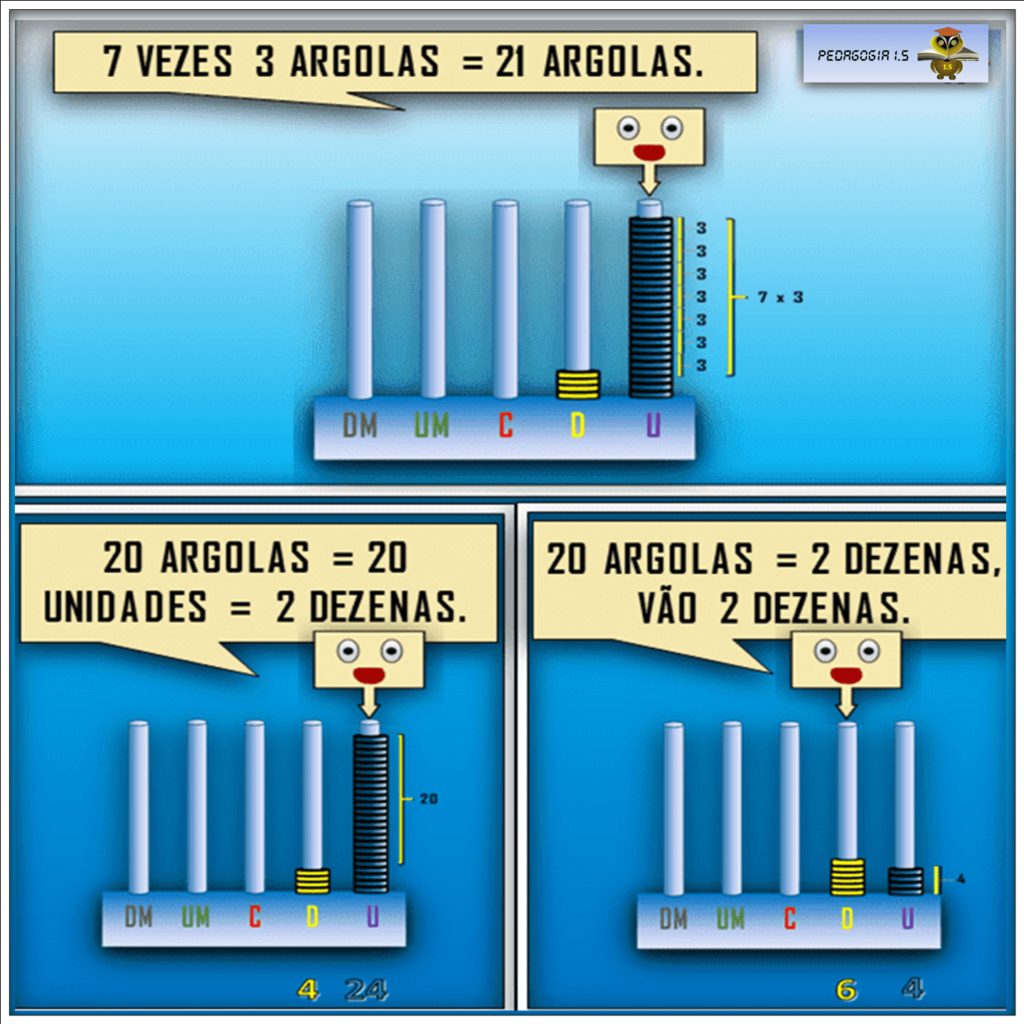
A figura acima ilustra as palavras de Piaget: o uso do ábaco para as primeiras operações numéricas, no caso da imagem, a soma.
A leitura do resultado da soma se faz a partir dos objetos materiais: no caso da soma, os objetos materiais são as argolas: são as quantidades somadas.
Essa soma é a quantidades, de objetos, de argolas, por isso, é como se fosse uma abstração empírica, isto é, uma abstração pseudoempírica.
É abstração pseudoempírica porque as propriedades que se constatam, isto é, a soma é algo que se faz na mente: a soma não está no ábaco, mas na mente daquele que soma.
O ábaco surgiu por volta do 3º milênio antes de Cristo. É um dos artefatos inventados pelo ser humano para efetuar cálculos.
A primeira máquina de calcular foi a mão, como nos informa Ifrah.
Porém, só temos dez dedos nas mãos e dez nos pés. Para quantidades maiores que vinte, o ser humano foi inventando outros artifícios para contar, para calcular.
As pedras serviram como instrumento de contar grupos maiores usando a estratégia da correspondência um a um: para cada pedra uma ovelha, por exemplo.
Grandes quantidades exigiriam também grandes quantidades de pedras. Criou-se outra forma de contar fazendo-se traços, riscos em pedras, madeiras, ossos, argila e mesmo nós em corda.
Os montes de pedras para contabilizar quantidades evoluíram para colunas de pedras em que aparece o Valor Posicional: unidades, dezenas, centenas da direita para a esquerda. Daí, originou-se o ábaco.
Por que Piaget. recomendou o uso do ábaco? A criança do período das operações concretas, por fazer abstrações pseudoempíricas, devido a sua imaturidade cerebral, não consegue fazer abstrações refletidas, próprias das contas de multiplicar.
No ábaco, o aluno consegue “ver” as unidades, dezenas, centenas etc. Também, visualizar o reagrupamento, o “vai um”, as trocas entre as argolas.
Ou seja, o aluno, professora, apoia-se no concreto para fazer abstrações. Por isso, são abstrações pseudoempíricas: são falsamente empíricas, pois o aluno faz operações mentais com base no concreto.
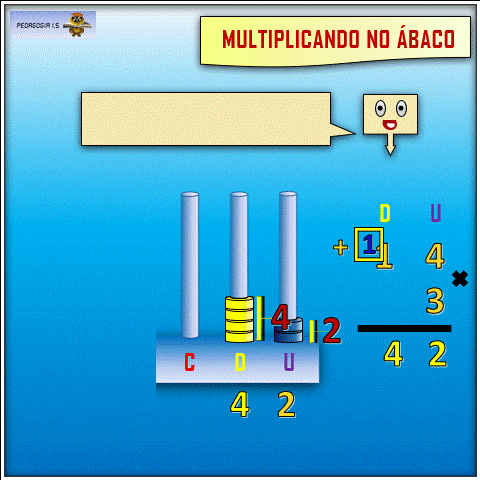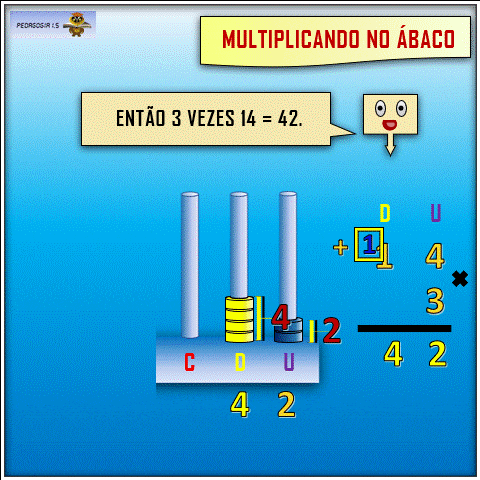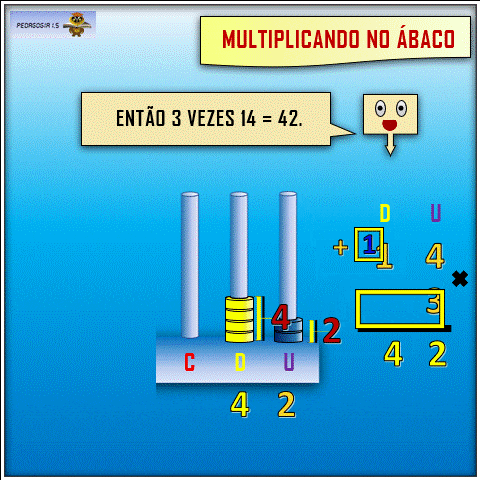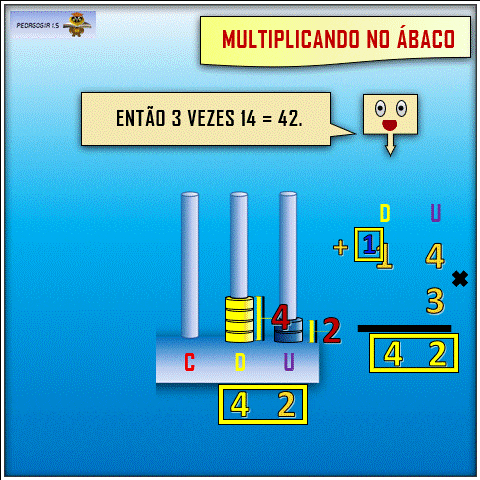
De Forma Simples, a Conta de Multiplicar Fica Mais Fácil Para o Aluno do 3º Ano do EFI ao Usar o Ábaco
Quando multiplicamos, por exemplo, 2 vezes 678, usando o algoritmo tradicional, a conta de multiplicar, não pensamos, professora, no seu procedimento altamente abstrato.
Fazemos assim: escrevemos o número 678 e embaixo do algarismo 8 escrevemos o 2. Fazemos um traço sob o 2 e colocamos um x para indicar a operação de multiplicar.
Veja, professora, que estamos trabalhando não com quantidades, mas com símbolos e símbolos são signos, que são abstrações, produtos criados pela mente humana.
Depois, começamos a técnica, o passo a passo, para fazer a conta:
● Dizemos: 2 vezes 8 é igual a 16;
● Escrevemos o 6 embaixo do traço, na direção do 8;
● Falamos: “vai 1”. Observe, professora, que falamos o valor absoluto do número: vai o número 1, quando, na realidade, estamos operando seu Valor Posicional, e deveria ser dito: vai 1 dezena;
● Então, multiplicamos 2 vezes 7 é igual a 14;
● Somamos: 1 mais 14 é igual a 15 e escrevemos 5 na frente do 6;
● Multiplicamos 2 vezes 6 é igual a 12 mais 1, 13;
● Escrevemos o 13 na frente do 5 e o resultado da multiplicação é 1356.
Note, professora, que o procedimento descrito dessa forma é muito, muito abstrato.
É uma técnica altamente complexa e sofisticada que o aluno precisa memorizar. Sem contar que a memorização das tabuadas do 7, 8 e 9 é das mais difíceis, e os alunos encontram bastante dificuldade.
A multiplicação no ábaco, porém, professora, fica muito mais fácil e evidente. Veja exemplos aqui e aqui, pois o aluno consegue visualizar as quantidades de argolas sendo movimentadas, o que deixa o processo menos abstrato, mais concreto.
O Que Você Pode Fazer Para Implantar Todo Esse Processo?
Faça Pedagogiação1.5.

A primeira professora coloca sua dúvida e a segunda professora mostra uma solução.
Como você está lendo este texto, professora, é provável que tenha chegado aqui por meio do Pinterest.
Se, sim, mostra que você exerce seu papel de pesquisadora. Põe em prática o seu lado de Cientista da Educação. Relembrando que ao fazer Pedagogia – sendo esta a Ciência da Educação – você se licenciou para ser uma Cientista da Educação.
A Cientista da Educação usa sua sala de aula como Laboratório de pesquisa e experimentação.
Sua busca por novos materiais de ensino é uma Pedagogiação: uma ação pedagógica consciente e intencional que visa levar seu aluno a um aprendizado mais efetivo.
É uma Pedagogiação, porém, ela precisa se transformar, ser aprimorado para uma ação pedagógica consciente, intencional e cientificamente orientada, porque ancorada em um Ensino Orgânico. Isso você consegue com a Pedagogiação1.5.
A ação pedagógica cientificamente orientada, a Pedagogiação1.5, está fundamentada em quatro áreas científicas:
● Semiótica: a Matemática trabalha com símbolos. A linguagem matemática é simbólica, e a Semiótica, auxilia a compreender bem os símbolos, pois é a ciência dos signos;
● Psicanálise: os erros nas contas de multiplicar, para além do desconhecimento do aluno nos princípios básicos da disciplina, também ocorrem devido à Ansiedade Matemática.
A Educação Narrativa, utilizando a História da Matemática, ajudará você, professora, a diminuir os níveis da Ansiedade Matemática de seus alunos.
● Psicogenética: compreender que seu aluno do 3º ano do Ensino Fundamental I faz abstrações pseudoempíricas e por isso precisa usar o material concreto vai facilitar muito seu processo de ensino-aprendizagem, professora.
● Neurociência Cognitiva: o que a Psicogenética piagetiana já havia demonstrado com a teoria das abstrações e sua prática, a Neurociência Cognitiva confirmou a respeito da imaturidade biológica do aluno.
O aluno do 3º ano do Ensino Fundamental I ainda não desenvolveu seu cérebro para efetuar contas tão abstratas e complexas como as de multiplicação, próprias do período das operações formais.
A Pedagogiação1.5 é uma ferramenta poderosa para auxiliar você, professora, em sua ação pedagógica.
Ferramenta que nasceu no Laboratório de Iniciação Científica com alunas e alunos de Pedagogia o LAPAPIEF – Laboratório de Pesquisa para Ação Pedagógica Interdisciplinar no Ensino Fundamental.
Das Oficinas do LAPAPIEF surgiu um método Inovador, Único, Revolucionário: a Pedagogia1.5.
A Pedagogia1.5 tem como ferramenta fundamental a Pedagogiação1.5, ou seja, a ação pedagógica consciente, intencional, cientificamente orientada porque orgânica que se estrutura a partir de cinco pilares:
1. Educação Narrativa: apoiada na História da Matemática para sustentar o ensino e aprendizagem da Matemática. A Educação Narrativa, individualmente, auxiliará, você, professora, a trabalhar com o aluno a questão da burrice em Matemática;
2. Agrupamento: a base da Matemática é o Agrupamento. Contar, calcular, é fundamentalmente agrupar, reagrupar e desagrupar. Somar e multiplicar é agrupar. Subtrair e dividir é desagrupar.
3. Valor Posicional: outro fundamento matemático é o Valor Posicional. A posição que o algarismo ocupa no número. O mesmo algarismo, 3 por exemplo, vale a unidade, a dezena, a centena conforme o lugar, a posição que ocupa no número.
4. Sistema de Numeração Decimal: tanto o Agrupamento quanto o Valor Posicional são a estrutura do Sistema de Numeração Decimal (SND). O desconhecimento desse sistema é uma das razões dos erros contínuos dos alunos nas contas.
5. Material Concreto: a necessidade de usar material concreto foi comprovada também cientificamente pela Neurociência Cognitiva, confirmando as teorias e práticas piagetianas na Psicogenética. Material dourado, ábaco e vídeos são imprescindíveis para alcançar um bom resultado no ensino-aprendizagem.
Você, professora, pode ter uma amostra totalmente GRATUITA da Pedagogia1.5 e de sua ferramenta principal a Pedagogiação1.5 no Minicurso GRATUITO Pedagogia1.5.
Referências
BECKER, Fernando. Abstração pseudo-empírica e reflexionante: significado epistemológico e educacional. Shème: Revista Eletrônica de Psicologia e Epistemologia Genética, v. 6, Edição Especial, nov. 2014, p. 104-128. Disponível em: < http://www.bjis.unesp.br/revistas/index.php/scheme/article/view/4276/3105 >. Acesso em: 02 mar. 2023.
IFRAH, George. História Universal dos Algarismos. Rio de Janeiro: Nova Fronteira, 1997.
PIAGET, J.; SZEMINSKA, A. A gênese do número na criança. Rio de Janeiro: Zahar, 1981.
ZATTI, F.; AGRANIONIH, N. T.; ENRICONE, J. R. B. Aprendizagem matemática: desvendando dificuldades de cálculo dos alunos. In: PERSPECTIVA, Erechim. v.34, n.128, p. 115-132, dezembro/2010. Disponível em: < https://www.uricer.edu.br/site/pdfs/perspectiva/128_142.pdf >. Acesso em: 19 set. 2022.