
VOCÊ ESTÁ PRESTES A DESCOBRIR OS 8 ATRIBUTOS MENTAIS QUE AUXILIAM O ENSINO DE ATIVIDADES DE MATEMÁTICA ESCONDIDOS NA PEDAGOGIAÇÃO 1.5
Pedagogiação1.5: ação pedagógica cientificamente orientada, intencional, consciente e orgânica que usa Vídeos-oficinas como ação didática e ajudam a desenvolver 8 atributos mentais essenciais para o ensino-aprendizagem de atividades de Matemática para o Ensino Fundamental 1.
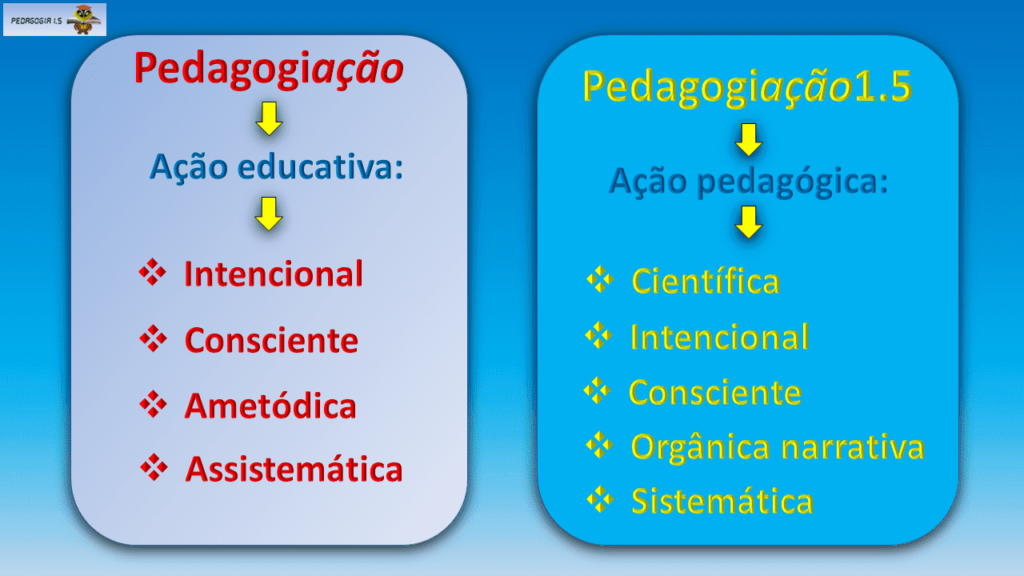
Em primeiro lugar, professora, é bom ter claro o que é ação pedagógica.
A ação pedagógica seria o lado concreto do processo educativo em que teorias educacionais são colocadas em prática.
Quando você, professora, pega atividades de matemática no Pinterest para usar em sala de aula, como você faz isso?
Há na sua ação, evidentemente, intencionalidade: você intencionalmente procurou atividades matemáticas para aplicar. Também, foi uma busca consciente. Então você fez uma Pedagogiação: ação intencional e consciente.
Esta é uma ação que pode ser chamada de ação educativa, se foi feita de forma não metódica e assistemática, nos dizem Dalbosco, Bertotto e Schwengber.
Isso ocorre se você busca as atividades sem um método, sem um planejamento. Uma ação em que o aluno aprenderá, porém, de forma superficial, pois apenas fará a atividade, mas não haverá um aprofundamento da questão.
Já a Pedagogiação1.5 é uma ação pedagógica cientificamente orientada, intencional, consciente e orgânica.

A Pedagogia 1.5 é resultado de 20 anos de docência em uma Faculdade de Pedagogia e 10 anos de Iniciação Científica.
Uma aluna e um aluno, em momentos distintos, perguntaram como ensinariam matemática se não sabiam a disciplina.
Nascia o LAPAPIEF – Laboratório de Pesquisa para Ação Pedagógica Interdisciplinar no Ensino Fundamental.
O objetivo do Laboratório: trabalhar com alunas e alunos a matemática. A síntese é o curso As Quatro Operações Matemáticas Fundamentais.
Você, professora, é uma Cientista da Educação. Relembre que Pedagogia quer dizer Ciência da Educação. Você passou alguns anos em uma faculdade de Pedagogia estudando inúmeras teorias que capacitaram você a aplicar essas teorias em sala de aula.
É ação pedagógica orgânica porque segue as diretrizes do Ensino Orgânico. É uma ação didática, porque cientificamente orientada, já que estabelece os caminhos teóricos que estruturam a ação pedagógica.
Não é uma ação pedagógica ametódica e assistemática, porém, metódica e sistemática. Segue uma orientação científica, planejada, objetivando atingir um fim educacional em que o aluno realmente aprenda.
Ação, seguindo o pensamento aristotélico, visaria um fim: quando o ser humano direciona suas ações para uma finalidade.
Há em toda ação uma intencionalidade, professora, inseparável dessa ação. Ela é praticada tendo por fim um objetivo partindo de alguma coisa que se deseja obter com tal ação.
A Pedagogiação1.5 segue essa intencionalidade de mediar o ensino e aprendizagem.
Busca fugir da ação pedagógica como violência simbólica como ensinava Bourdieu. O ensino tradicional impõe significações aos alunos como se fossem legítimas.

Pense, professora, na violência simbólica que é o ensino dos algoritmos, das contas, que a escola impõe aos alunos.
Lembremos que os alunos do Ensino Fundamental I estão na fase das operações concretas e suas mentes operam com abstrações pseudoempíricas.
Os algoritmos, as contas, são da fase das operações formais em que a mente do aluno opera com abstrações reflexionantes.
Isso é uma verdadeira violência simbólica. Não apenas simbólica, mas também fisiológica.
A escola tradicional vem violentando a fisiologia cerebral do aluno que ainda não tem maturidade física e cerebral para compreender abstração reflexionante que estrutura a conta, o algoritmo, conforme mostra a Neurociência Cognitiva.
Outra face da violência simbólica, que a escola impõe ao aluno, é sua exclusão do processo ensino-aprendizagem
A escola tradicional separa ensino e aprendizagem. O primeiro fica a cargo do professor e o segundo é de responsabilidade do aluno.
O professor ensina sempre, mas é o aluno que não aprende.
Os alunos não participam do processo de ensino, são meros participantes, observadores, sempre estáticos, sentados em frente do docente, objetos manipulados pelo professor e a escola
Penso que para eliminar a violência simbólica, devemos pensar na ação comunicativa comandando as ações didática e pedagógica, conforme propõe Zaslavsky (2017, p. 75).
Para o autor, a ação pedagógica tem sido vista de forma unidirecional e não de maneira interativa.
A ação pedagógica não deve ser sinônimo de ação docente, mas uma articulação efetiva da ação do professor com a ação do aluno, mediante a busca de entendimento.
Na relação professor-aluno há um desequilíbrio de conhecimento entre docente e aluno, ou seja, ela é assimétrica.
Por isso, a ação comunicativa seria a responsável por coordenar ações que orientem o entendimento professor-aluno.
No ensino tradicional, o aluno não é participante: é objeto passivo. A ação comunicativa, coordenando ações e orientando-as pelo entendimento, leva professor e aluno a se compreenderem mutuamente.
A ação pedagógica deve ser propriamente uma interação pedagógica, pontua Zaslavsky.
A Pedagogiação1.5 aceita e propõe esse caminho interativo. Uma interação, ação entre, professor e aluno em busca de um Ensino Orgânico, usando a Educação Narrativa.
Não sei para você, professora, mas a expressão planejamento escolar costuma causar urticária em muitos professores.
Lembra aquele período chato de início de ano letivo, quando ainda sem alunos, os professores são obrigados a elaborar seu planejamento escolar.
A maioria apenas copia o planejamento do ano anterior que estava esquecido em uma gaveta ou pasta. Seria somente um trabalho mecânico visando cumprir uma exigência burocrática da legislação escolar.
Professora, porém, planejamento é vida. Viver é planejar. Se você não planeja, sua vida cotidiana se transforma em um caos.

Planejamos de forma quase instintiva. Na realidade, nem percebemos o quanto planejamos as nossas tarefas. A figura acima, editada pela Pedagogia1.5, ilustra bem isso.
A ordem que você, professora, estabelece na sua rotina diária é produto de um planejamento que se tornou habitual e que organiza seu cotidiano.
Suponhamos que você necessite comprar uma determinada roupa. O que você faz? Planeja:
● Economicamente: planeja quanto vai gastar, se será a vista ou se usará o crediário.
● Esteticamente: planeja que tipo de roupa lhe cairá melhor, a cor que possibilitará realçar determinados atributos seus ou que combinará com certa bolsa ou sapato.
● Sazonalmente: se a roupa, por exemplo, for para um casamento, qual a estação do ano? A roupa terá que se adequar à temperatura: o tecido, o modelo.
● Geograficamente: e de forma mais prática, em que lugar irá comprar, como chegará lá. Aliás, no geral, mentalmente você planeja seu trajeto: vou pela rua tal, viro em tal esquina, corto este caminho para ganhar tempo etc.
● O meio de transporte: se vai de carro, onde estacionar, se pagará ou não o estacionamento; se for de ônibus, qual irá pegar, onde irá pegar, onde descerá, qual o local mais perto.
Normalmente, não pensamos nisso. Porém, a simples compra de uma roupa nos faz, quase automaticamente, efetuarmos todo esse planejamento.
Então, por que uma aula a ser ministrada seria diferente?
Muitos professores, entretanto, apenas rotinizam uma experiência escolar.
Até pouco tempo atrás, bastava um giz, uma lousa, um livro didático para passar a lição na lousa para que os alunos copiassem.
Hoje, se usa as novas tecnologias: a tecnologia da xerocópia. Copia-se uma atividade que serão distribuídas aos alunos e coladas em seus cadernos.
Essa pode ser apenas uma ação educativa e não uma ação pedagógica.
Na Pedagogiação, apenas uma ação educativa, muitas vezes intencional e consciente: vou pegar uma atividade de divisão para trabalhar amanhã. Mas qual o objetivo específico a ser trabalhado? Qual habilidade a ser desenvolvida?
Isso nos remete ao pensamento de Arendt: É muito fácil, porém, ensinar sem educar, e pode-se aprender durante o dia todo sem por isso ser educado (Hannah Arendt, 2011, p. 247)
A ação educativa ensina, mas não educa. Por isso, os alunos, muitas vezes, aprendem a técnica do algoritmo, apenas repetem a técnica, mas desconhecem os fundamentos básicos do ensino matemático.
A Pedagogiação1.5 propõe, por isso mesmo, um planejamento orgânico.
O que seria o planejamento orgânico?

A professora necessita ter clara a questão da intencionalidade de sua ação pedagógica. Despertar a Cientista da Educação adormecida para fundamentar teoricamente o que vai ensinar para garantir uma ação pedagógica consistente.
O planejamento orgânico não é um exercício técnico, mas analisar o conteúdo matemático a ser ensinado, refletir sobre a realidade de seus alunos e prever uma ação, inclusive maneiras alternativas de ação a fim de suplantar possíveis dificuldades.
As perguntas chaves são:
● O que ambicionamos realizar? Ou seja, quais objetivos queremos alcançar.
● O que e como vamos fazer? Quais são os procedimentos necessários para atingir os objetivos.
Ao planejarmos organicamente uma atividade de matemática, principalmente no Ensino Fundamental I, devemos levar em consideração alguns atributos mentais necessários para o bom desempenho dos alunos.
Esses atributos mentais são enumerados de forma bem geral por Silva em sua Dissertação de Mestrado.
Para que haja Pedagogiação1.5, os atributos mentais devem ser desenvolvidos. Basicamente, os atributos mentais são:
1. Senso numérico;
2. Capacidade numérica;
3. Capacidade algorítmica;
4. Capacidade de trabalhar com abstrações;
5. Senso de causa e efeito;
6. Capacidade de organizar e acompanhar uma sequência causal de fatos ou eventos;
7. Capacidade de raciocínio lógico;
8. Capacidade de raciocínio relacional.
A seguir, vamos detalhar melhor cada atributo mental. Acrescentarei alguns exemplos para o ensino de Matemática no Ensino Fundamental I. Acompanhe:
1. Senso numérico
É a capacidade de saber a diferença entre um objeto, grupos de 2, 3 e 4 objetos. Perceber que um agrupamento possui mais elementos que outro agrupamento. Ter a percepção que um pequeno grupo muda quando se acrescentarem ou retirarem um ou mais objetos.
O Sistema de Numeração Egípcio é um exemplo de como o senso numérico facilita a leitura do número:
Observe, professora, que a leitura dos 9 traços que indicam os nove primeiros números egípcios é confusa.
O que fizeram os matemáticos egípcios, separaram os 9 traços em pequenos agrupamentos de 2, 3 ou 4 para facilitar a leitura.
O senso numérico é essa percepção direta de pequenas quantidades sem a necessidade de contar cada elemento do grupo.
Separamos este artigo que pode ajudar você a entender melhor o senso numérico:
- Porque Entender o Agrupamento Ajuda no Ensino das Atividades de Matemática
2. Capacidade numérica
É a aptidão de contar, indefinidamente, grandes quantidades.
Processo que compreende, professora, ordenar os objetos de um grupo de certa maneira, e, depois, empregar essa ordenação para contar todos esses objetos, um a um ou dois a dois ou três a três ou conforme outro agrupamento.
Vai além do processo da correspondência um a um, pois utiliza um procedimento de contagem.
Mesmo povos que não usam o Sistema de Numeração Decimal, o SND, avaliam grandes quantidades usando a capacidade numérica.
Os Malgaxes, professora, enfileiram seus guerreiros cada um com uma pedra. Coloca-os em fila e cada um passa por determinado lugar colocando sua pedra. Quando chega ao grupo de 10, este é trocado por uma pedra e colocado em outro poço.

Se ao final, tiverem 3 pedras no poço da direita, 4 no poço anterior e 2 no poço anterior a este, sabem que sua quantidade equivaleria a 243 guerreiros se fosse no SND.
3. Capacidade algorítmica
É a competência de executar processos. O algoritmo nada mais é que uma sequência de passos que devem ser seguidos para se atingir um determinado objetivo.
O Sistema de Numeração Decimal culminou, professora, no algoritmo. A História da Matemática prova isso.
Qualquer receita alimentícia é um algoritmo. Um passo a passo de como agrupar determinadas quantidades de alimento em uma vasilha, misturá-los para obter certa consistência e depois cozinhar, assar ou não para alcançar o objetivo da receita.
Para a Pedagogiação1.5, o algoritmo, a conta, não deve ser ensinada sem contextualização.
A contextualização proposta pela Pedagogiação1.5 é narrativa histórica. A narrativa torna a abstração do algoritmo algo concreto.
A conta de dividir, que engloba as outras três operações, só foi possível historicamente com o SND.
É um processo técnico que demandou milênios para ser construído.
Necessita da abstração reflexionante que, relembremos, os alunos do Ensino Fundamental 1 ainda não desenvolveram, pois estão no período das operações concretas que trabalha dentro da abstração pseudoempírica.
Por isso, Piaget recomenda o uso do ábaco para se trabalhar atividades de Matemática com as crianças desse período.
4. Capacidade de utilizar abstrações
A realidade é o concreto e desvincular alguma coisa da realidade, desse concreto, separando, isolando de outras coisas, e fazer operações mentais, trabalhando conceitos, ideias traduz a capacidade de abstrair.
Abstrair significa tirar algo de alguma coisa, separar, analisar. É operação mental, trabalhar na mente algo fora da realidade.
O algoritmo, por ser uma técnica, é pura abstração. Abstração reflexionante em que se opera no campo de coordenações de ações na mente.
Como visto, a criança do Ensino Fundamental I não tem maturidade fisiológica para operar completamente a abstração reflexionante. Por estar no período das operações concretas, utiliza a abstração pseudoempírica: precisa se apoiar no concreto.
O “vai um” representa um exemplo perfeito da Abstração Reflexionante. Quando o professor diz “vai um”, ele está abstraindo, usando o valor absoluto do algarismo, o um, em lugar do seu valor relativo, pois o que vai é a dezena, por exemplo.
Isso causa um confusão na cabeça da criança. Ela não entende essa operação, operação formal, enquanto ela necessita, para operar abstratamente de se apoiar no concreto.
Bill Waterson mostra esse processo na tirinha em que o Calvin, conversando com o Haroldo fala que a Matemática é uma religião:
5. Senso de causa e efeito
Ter a percepção de que determinados acontecimentos causam ou desencadeiam novos acontecimentos.
A tirinha do Calvin, acima, ajuda a entender.
Por que o Calvin acha que a Matemática é uma religião? Ele percebe essa falta de senso de causa e efeito no ensina da Matemática.
Por que um número, milagrosamente, de repente, vira outro número?
No “vai um”, é isso que parece acontecer para a criança. Um número vai para onde? É como um milagre.
Os estudos piagetianos enfatizam a lógica do pensamento infantil. No Ensino Fundamental I, as crianças usam a lógica operatória, ou seja, sua lógica necessita ser ancorada no concreto, na experiência vivida.
O “vai um”, resultado da lógica formal, das operações abstratas, é um afastamento da experiência, concreta, sendo um operação mental simplificadora que facilita se efetuar a conta, o algoritmo.
6. Capacidade de organizar e adotar uma sequência causal de fatos ou acontecimentos
Uma demonstração matemática depende dessa capacidade. Quando um feirante calcula mentalmente o troco ele está se utilizando dessa capacidade.
Aqui, entram as tão incompreendidas e menosprezadas propriedades matemáticas que tanto auxiliam o cálculo mental.
Quando um aluno diz não saber o resultado da tabuada de multiplicação, por exemplo, 7 x 9, ele não compreende que sabe sim esse resultado.
As tabuadas de multiplicar até o 5, geralmente, são de fácil domínio. Se o aluno usasse a propriedade associativa, ele faria facilmente o cálculo, pois 7 vezes 9 é igual a 3 vezes 9 mais 4 vezes 9.
7. Capacidade de raciocínio lógico
É a competência de organizar ou estruturar diversos raciocínios que nos possibilita, seguindo certas regras, alcançar uma conclusão ou resolver um problema.
Ao contrário do que imaginam muitos professores, efetuar contas não desenvolve o raciocínio lógico.
A conta, o algoritmo, por ser apenas uma técnica pode ser efetivada, simplesmente, se decorando o procedimento sem uma tomada de consciência do processo.
Falando aos pedagogos, Piaget adverte: Pouco importa que a criança saiba repetir
fórmulas exatas, se elas não correspondem a um esforço de verificação livre. (Piaget, 2009, p.342).

A conta ou algoritmo é uma técnica, um passo a passo capaz de ser decorado. Decorar não promove o raciocínio lógico.
Na figura, o Paulo apenas repete o passo a passo para a conta de multiplicação. Qualquer aluno, em qualquer lugar, vai seguir esses mesmos passos para efetuar essa conta.
A Joana, por outro lado, professora, escolheu uma das propriedades da multiplicação e raciocinando logicamente efetuou a operação.
8. Capacidade de raciocínio relacional
Quando o aluno aprende o sinal de igual, ele começa a estabelecer que existe uma relação de que, por exemplo, um quantidade é igual a outra.
Que entre 4 maçãs e 4 balas, há uma relação de igual referente às quantidades: são quatro para cada uma.
Estabelecer uma relação entre um número e um símbolo indica a capacidade relacional do aluno.
Além de perceber que entre o símbolo e o número existem propriedades que são próprias deles.
Ao somar 8 + 4 = 12, o aluno percebe que se trata de um todo e não de partes independentes uma da outra.
A Pedagogiação1.5, para facilitar a aprendizagem da capacidade relacional, utiliza a Leitura de Imagem.
A imagem auxilia nesse processo ao tornar concreto algo que é abstrato.
O sistema monetário é um ótimo exemplo de como tornar o abstrato algo concreto para o aluno.
A criança aprende a lidar com o dinheiro na vida prática e ao igualar, na leitura de imagens, 5 moedas de 1 real a 1 nota de 5 reais, ela vê, na prática, essa capacidade relacional.
Referências
ARENDT, Hannah. A crise na educação. In: Entre o passado e o futuro. São Paulo: Perspectiva, 2011.
DALBOSCO, Claudio A.; BERTOTTO, Cláudio; SCHWENGBER, Ivan L. A ação pedagógica crítica e formação do pensamento reflexivo. In: Olhar de Professor, vol. 23, pp. 01-14, 2020. Disponível em: < https://www.redalyc.org/journal/684/68464195054/html/#redalyc_68464195054_ref19 >. Acesso em: 27 abr. 2022.
PIAGET, Jean. O egocentrismo. In: Silvia Parrat-Dayan. Piaget na Ecole Libératrice: a dialética do outro e do mesmo. Schème. Revista Eletrônica de Psicologia e Epistemologia Genéticas. Volume 2 Número 3 – Jan-Jul/2009. Disponível em: < https://www.marilia.unesp.br/Home/RevistasEletronicas/Scheme/Vol02Num03Traducao.pdf >. Acesso em: 03 mai. 2022.
SILVA, Ramalho Garbelini. Sistemas de Numeração: Das Talhas Numéricas aos Primórdios da Computação Artificial. 2016.147 f. Dissertação (Mestrado) – Universidade Federal de Juiz de Fora, Instituto de Ciências Exatas. PROFMAT – Mestrado Profissional em Matemática em Rede Nacional, 2016. Disponível em: < https://repositorio.ufjf.br/jspui/handle/ufjf/3265 >. Acesso em: 10 abr. 2022.
ZASLAVSKY, Alexandre. Ação pedagógica, ação comunicativa e didática. In: Conjectura: Filos. Educ., Caxias do Sul, v. 22, n. 1, p. 69-81, jan./abr. 2017. Disponível em: < http://educa.fcc.org.br/pdf/conjectura/v22n1/2178-4612-conjectura-22-01-00069.pdf >. Acesso em: 27 abr. 2022.



