A PROVA DE QUE O ALUNO NÃO ERRA MAIS AS CONTAS EM ATIVIDADES MATEMÁTICAS É ENTENDER BEM O SISTEMA DE NUMERAÇÃO DECIMAL
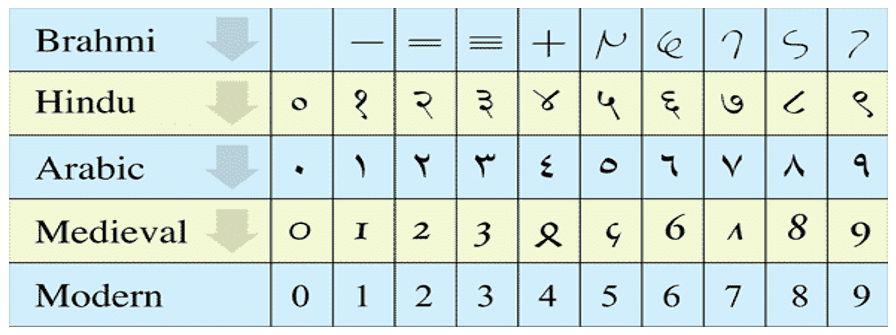
O Sistema de Numeração Decimal (SND) é o sistema que usamos para contar e efetuar cálculos. Foi uma invenção histórica do ser humano e criado durante milênios tendo como base o Sistema de Numeração Indu que foi trabalhado e divulgado pelos árabes no Ocidente.
O ser humano é o único animal simbólico, professora, pois detém a capacidade de produzir símbolos para se comunicar.
Também produz informações úteis que armazena e transmite para as gerações posteriores.
Entre essas informações encontra-se a matemática, uma linguagem, que trabalha com quantidades. Houve uma infância da matemática que se perde nas noites do tempo.
Avaliar uma quantidade, professora, isto é, quantificar, é uma necessidade humana. Os números fazem parte indiscutível de nosso dia a dia.
Estamos tão acostumados com os números que nem notamos que houve uma época em que os seres humanos não sabiam contar.
Encontram-se, hoje em dia, professora, certas tribos indígenas que utilizam apenas dois nomes de números para contar: dois-um para quantificar o três e dois-dois para o quatro.
A fim de expressarem um número maior, apontam para os cabelos, para indicar inúmeros, de acordo com os fios de cabelos em sua cabeça.
Contar faz parte, exclusivamente, da vida humana. Mas alguns animais possuem senso numérico, como os corvos, que conseguem perceber até a quantidade de quatro objetos.
Para nossa percepção é extremamente fácil percebermos, sem contar, até quatro objetos. É o que se chama senso numérico.
Saiba Exatamente o Que É a Correspondência Um a Um
Quantificar é uma necessidade. Um pastor de ovelhas, professora, por exemplo, enquanto convive com um número pequeno de ovelhas, guarda na memória quais são, devido a sua familiaridade com elas.
Porém, quando seu número aumenta, necessita de algum artifício para saber se todas estão juntas. Recorre, então, professora, à correspondência um a um.
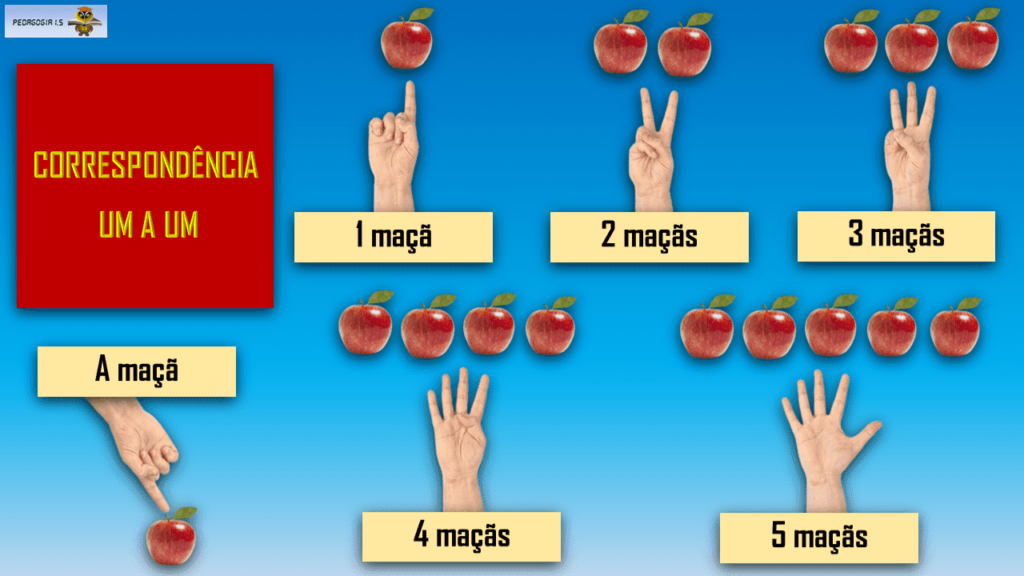
Ifrah (1997) anota a maravilhosa eficácia e mobilidade da mão, o que a torna, a primeira máquina de contar ou calcular da humanidade.
A correspondência um a um mostra-se como a forma mais elementar de contagem, quando um dedo corresponde à unidade, e os outros dedos vão se somando correspondentemente aos objetos que se deseja contar.
Usam-se os dedos das duas mãos; depois os dedos dos pés para essa correspondência até uma quantidade de vinte unidades.
As falanges dos dedos, professora, também foram utilizadas, na Índia, China e Indochina, para a contagem na correspondência um a um, perfazendo-se um total de 28, ao se utilizar todas as falanges das duas mãos.
A correspondência um a um pode ser considerada o primeiro procedimento aritmético da História, como pondera Ifrah (1997).
Trata-se de um modo de comparar dois grupos de coisas ou seres sem a necessidade de usar a contagem abstrata. A correspondência um a um opera com o concreto.
O autor exemplifica o processo, professora, em tempos contemporâneos com o bilheteiro do cinema: munido de um mapa com o número de assentos, vende os bilhetes e marca em cada local, no mapa, o bilhete vendido.
Quando todos os lugares no mapa estiverem preenchidos, a lotação da sala estará completa.
Este artificio possibilitou ao ser humano praticar a aritmética desde a Pré-história sem que ainda houvesse inventado o número abstrato.
O pastor de ovelhas criou um mapa de contagem, usando a correspondência um a um, quando, não sabendo contar o seu rebanho, percebe apenas que são muitos.
Um deles inventou um procedimento concreto: a prática do entalhe. A cada ovelha que entra no abrigo, usa uma pedra afiada para fazer um entalhe num osso. O número de entalhes representa o total de ovelhas que tem.

Esse osso entalhado representa a memória concreta de seu rebanho. Basta deslizar o dedo sobre cada entalhe, ao entrar um carneiro, para perceber se todos estão ou não ali no abrigo.
A correspondência um a um é uma abstração realizada a partir de elementos concretos. É a comparação mental entre elementos de dois grupos diferentes.
Trata-se, porém, de um procedimento propício apenas para pequenos grupos de coisas.
Um osso com vinte entalhes, por exemplo, serve como modelo para coleções de vinte coisas diferentes, sejam vinte seres humanos, vinte ovelhas, vinte dias.
Diversos materiais serviram para efetivar a correspondência um a um: pedras, frutos duros, paus, cocos, dentes de elefantes, grãos diversos, bolas de argila.
A Verdade É Que o Corpo, Principalmente as Mãos, Ajudou a Construir os Números
O corpo representa outra maneira utilizada pelos povos antigos indígenas para a correspondência biunívoca (um a um). Povos da Oceania assim procedem:
Tocam-se os dedos um a um, depois o pulso, o cotovelo e o ombro do lado direito do corpo, depois o esterno, depois as articulações do lado esquerdo sem esquecer os dedos da mão esquerda. Obtém-se assim 17. Se isso não basta, acrescentam-se os dedos do pé, o tornozelo, o joelho e as nádegas (esquerda e direita). Obtém-se assim 16 a mais, portanto 33 ao todo. Para além desse número se é ajudado por um pacote de pauzinhos. (IFRAH, 1997, p. 25).
Algumas tribos indígenas, professora, usam o corpo para contar; e para cada parte enumerada dizem uma palavra. A palavra dita corresponde à parte do corpo tocada.
Encontram-se traços antropomórficos da gênese da contagem. Ifrah (1997) exemplifica com a língua ali, de um povo da África Central.
Eles usam as palavras moro e mbouna para designar cinco e dez. Moro, etimologicamente, significa mão e mbouna é contração de moro e bouna (dois), portanto mbouna = dez = duas mãos.
Para se construir um sistema numérico dois princípios são necessários: correspondência e sucessão. A cardinalidade e a ordinalidade.
Seus alunos, professora, costumam não saber a diferença entre cardinalidade e ordinalidade, mas, relembre como é simples.
O mês tem 31 dias. O 31 significa o número total de dias do mês: o cardinal. Mas 31 também aponta ser o trigésimo primeiro dia do mês: o ordinal.

Como argumenta o autor, a mão humana mostrou-se ser um instrumento natural, capacitando o ser humano a compreender os dez primeiros números da aritmética elementar.
A mão pode comportar-se, de modo bastante natural e simples, como uma máquina de contar. E apresenta de maneira intuitiva os dois princípios fundamentais da aritmética o cardinal e o ordinal.
Eves (2011) procura mostrar que a necessidade de se fazer contagens maiores leva a obrigação de se criar um sistema de numeração.
A correspondência um a um pode ser eficaz, porém não é eficiente, professora. Quanto maior o número de objetos a contar mais difícil se torna o processo.
Os marcadores que se usam para a contagem na correspondência um a um podem se esgotar: só temos 20 dedos, nem sempre se tem uma quantidade de pedras, ossos etc. suficientes para se comparar os objetos.
Preste Atenção Para a Forma Como Evoluíram as Bases
Uma questão deve ter surgido para os povos indígenas antigos, aponta Gundlach (1992): o que se deve fazer quando o número finito de marcadores (os dedos por exemplo) se esgota, porém, se tem objetos restantes que precisam ser contados?
Recorre-se a um sistema, criando-se um grupo básico. Os dedos de uma mão formam um grupo básico de cinco. Duas mãos, um grupo básico de dez. (EVES, 2011).
Estudos apontam que os números 2, 3, e 4 foram bases primitivas. Nativos de Queensland, por exemplo, professora, usam a base 2 e contam: um, dois, dois e um, dois e dois, muito.
O sistema de base 5, quinário, parece ter sido aquele mais usado. Algumas tribos da América do Sul utilizam as mãos e contam: um, dois, três, quatro, mão, mão e um etc.
Houve um sistema vigesimal, referente à base 20, um sistema sexagesimal, com base 60, usado pelos babilônios (EVES, 2011).
Mas histórica, geográfica e etnograficamente a base dez, o sistema de numeração decimal, tornou-se a mais difundida, sendo, fundamentalmente, hoje, quase universalizada.
Uma coisa é contar. Outra coisa, guardar o resultado da contagem. A memória humana falha. Daí a necessidade de registrar o processo da contagem. Mas como fazê-lo quando ainda não havia números?
Para registrar sua contabilidade, o ser humano inventou a prática do entalhe. Como diz Ifrah (1997), a prática do entalhe é modo de contar dos iletrados. Ela teria pelo menos quarenta milênios de existência.
Encontram-se entalhes nas paredes das cavernas datadas da era pré-histórica. Não permitem dúvida em relação ao seu emprego contábil.
Ainda recentemente, professora, indígenas americanos, nos arredores de Los Angeles, usavam entalhes em madeira para memorizar suas jornadas de trabalho: para cada dia um entalhe fino; para cada semana um entalhe mais grosso e cada quinzena contava com entalhe feito em cruz.
Como anota o autor, o ser humano aprendeu a contar e a mão constituiu a sua primeira forma de registro contábil. Mas por ser um suporte passageiro não resistia à memorização.
A evolução social, com o crescimento do artesanato e comércio, levou à necessidade de registrar suas atividades econômicas de forma permanente para um ser humano que ainda não sabia escrever.
A civilização Inca criou o quipu (palavra inca para nó). Era composto de um cordão principal onde eram amarrados barbantes mais finos de várias cores e agrupados segundo uma determinada ordem com nós diferenciados.

Os nós em corda não foram exclusividade dos Incas, mas encontram-se em regiões diversas, desde a Antiguidade, na Grécia, Palestina, entre os árabes, chineses etc.
Porém, essa memória gravada em pedras, argila, ossos, cordões, não foi suficiente. A linguagem articulada precisava de um instrumento de maior alcance: a escrita. Ela representa um testemunho permanente e durável.
As palavras desaparecem, professora, e na Antiguidade não podiam ser gravadas. A escrita veio cumprir essa função, tanto que Voltaire dizia que era a pintura da voz. Ela dá acesso ao universo do pensamento extrapolando tempo e espaço. (IFRAH, 2005).
Onde Você Pode Encontrar na Construção dos Números a Ajuda Para Diminuir os Erros nas Contas
A história da construção dos números surgiu há cerca de cinco mil anos. Sociedades mais avançadas sentiram a necessidade de guardar de forma permanente as informações relativas às quantidades.
A princípio as pedras com tamanhos diversos passaram a representar, usando a base dez, valores diferentes: uma pedra pequena representava a unidade, uma um pouco maior representando a dezena, outra maior para a centena e uma bem maior para o milhar etc.
Das pedras, as vezes difíceis de serem encontradas, passou-se para a argila: pequenos cones ou bastões representavam as unidades, bolinhas para dezenas e cones grandes para centenas etc.
Aos poucos foram sendo gravados entalhes na argila: um entalhe fino, unidade; pequena marca circular, dezena; grande marca circular, centena e ainda outras marcações.
Esses entalhes gravados na argila já são signos numéricos, pois cada marca representa um número e os tabletes de argila com as marcas gravadas podem ser lidos e correspondem a um apropriado sistema de numeração (IFRAH, 2005).
Os egípcios criaram o seu sistema de numeração fundamentado na base decimal. Eles usaram suporte diferente da argila, fizeram entalhes em pedras ou escrevendo em folhas de papiro. Isso ocorreu por volta de 3000 a.C.

Um documento histórico, considerado o primeiro, é a Paleta de Narmer. Foi esculpido em pedra no antigo Egito e servia para esmerilhar materiais minerais usados para confeccionar cosméticos.
A paleta traz figuras do faraó da 1ª Dinastia, Narmer. O nome acha-se esculpido em hieróglifos no alto da paleta: um peixe gato, do faraó que unificou o Baixo e o Alto Egito.
Esta paleta traz também esculpidas representações numéricas, provavelmente valores de resgate recebidos pelo faraó.
Pela representação vemos a quantidade de touros (400 000), cabras (1 422 000) e 120 000 prisioneiros.
O sistema de numeração egípcio constituía-se de sete números básicos: a unidade, a dezena, a centena, a unidade de milhar, a dezena de milhar, a centena de milhar e a unidade de milhão.
Para cada um desses números correspondia respectivamente um traço vertical, uma figura semelhante a ferradura, uma corda enrolada, a flor de lótus, o dedo indicador, um girino e um homem ajoelhado.
O sistema egípcio era aditivo, ou seja, usava a combinação de símbolos para a montagem dos números. Como a base era dez, não se repetia mais que 9 símbolos, pois 10 eram trocados por outro equivalente ao próximo agrupamento.

Outro sistema de numeração que ainda conhecemos e às vezes trabalhamos com ele é o romano.
Mostradores de relógios, capítulos de livro, datas, principalmente, as de séculos, continuam sendo representados por meio de algarismos romanos.
Os algarismos romanos não se propunham a realizar operações aritméticas. Serviam basicamente para registro.
O sistema de numeração romano também usa a adição, o princípio aditivo, quase sempre. Utiliza os seguintes símbolos:
● I = 1;
● V = 5;
● X = 10;
● L = 50;
● C = 100;
● D = 500 e
● M = 1000.
Os romanos criaram, também, a regra de subtrair. Assim um número colocado à esquerda de um número maior subtrai este. Para fazer 4, usa-se IV; para o 9, IX; para o quarenta, XL etc.
Finalmente! O Segredo do Sistema de Numeração Decimal
O nosso sistema de numeração decimal moderno é também conhecido como indo-arábico.
Nasceu perto do séc. V no norte da Índia. Aí se constituíram os fundamentos do cálculo escrito que usamos hoje.
Provém da antiga numeração hindu, que ao contrário das demais escritas, tem um caráter simbólico mais evidente.
Seus nove algarismos iniciais são signos independentes, não procuravam uma equivalência visual com o número correspondente. Por exemplo, tanto o 1 dos sistemas numéricos egípcio e romano tinham o traço vertical como protótipo.
Avançaram mais ao dar um nome para cada número escrito. Isto iria produzir uma revolução, pois abriu caminho para o Valor Posicional.
Ao contrário de nós, porém, para dizer o número 3709 por extenso – nós dizemos: três mil setecentos e nove – eles diziam nove, sete centos e três mil.
Simplificaram mais ainda e passaram a falar apenas as unidades dos números: nove, sete, três. Mas aí havia um problema. Ao falarem assim sugeria 379. O zero ainda não havia sido inventado.
Eles criaram então uma palavra para expressar a falta da unidade correspondente ao 0: vazio. Então diziam o número por extenso: nove, sete, vazio, três.
Com isso inventaram o Valor Posicional e descobriram o zero.
O Valor Posicional fica claro se pensarmos como os hindus no início: para dizerem por extenso 2222 diriam dois, dois, dois e dois. Observem que no numeral (o número 2 é o mesmo) o que muda é que ele vale, possui um valor diferente, em cada posição.
Hoje sabemos que o primeiro 2 da direita equivale à unidade, o segundo 2 corresponde à dezena, o terceiro 2, à centena, e o quarto 2, à unidade de milhar.
O império árabe em um século se expandiu com a força do islamismo e das armas, estendendo seu domínio da Índia à Espanha, Mesopotâmia, Pérsia e norte da África.
Quando os árabes entraram em contato com os algarismos hindu e sua aritmética, perceberam a sua superioridade e vantagens e passaram a adotá-lo. Isso por volta do século IX.
Em sua expansão conservaram e propagaram a cultura ocidental, apoderando-se dos saberes hindu e grego.
Durante o reinado de Al-Mâmûn (809 a 833), por sua ordem, muitas obras gregas foram traduzidas.
Em seu reinado um intelectual famoso Al-Khowârizmi escreveu um livro de estudos sobre numerais e um tratado de álgebra que tiveram forte influência europeia ao serem traduzidos para o latim no século XII. (EVES, 2011).
O livro sobre numerais hindus de Al-Khowârizmi criou uma palavra para o Ocidente: algoritmo, uma tradução do nome do autor e que ganhou o significado de calcular de uma forma particular.
Também Al-Khowârizmi gerou algarismo. Este escritor árabe foi o responsável pela introdução do sistema de numeração indo-arábico no Ocidente. Seu livro trata do Valor Posicional e ensina cálculos matemáticos.
Para uma melhor compreensão do Sistema de Numeração Decimal, vamos compará-lo ao sistema de numeração egípcio e romano.
O sistema de numeração decimal tem a base 10. Isso significa que as quantidades se agrupam e reagrupam de 10 em 10. No sistema egípcio a base também é 10 assim como no romano.
O SND (Sistema de Numeração Decimal) é posicional: 63 é completamente diferente de 36. O 3 tem um valor diferente de acordo com a posição que ocupa no número: em 63 ele representa três unidades em 36, representa três dezenas.

O sistema egípcio não é posicional. Para eles, tanto faz escrever o doze dessa forma ou dessa outra maneira.
O sistema romano também é posicional, pois VI é diferente de IV. O I antes do V subtrai, depois do V, adiciona.
No SND, temos um símbolo para o nada que é o zero; os sistemas egípcio e romano não têm.
O SND trabalha com o princípio multiplicativo: no sistema posicional o número 444, por exemplo:

Cada algarismo representa o produto dele mesmo pelo valor de sua posição.
O princípio multiplicativo não vale para os sistemas de numeração egípcio e romano.
O princípio aditivo é comum aos três sistemas que estamos comparando:

Outra comparação entre os sistemas de numeração é a quantidade de algarismos necessários para escrever qualquer número:
No SND, pode-se escrever qualquer número usando-se dez símbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Isso torna o sistema expressivamente eficiente e eficaz. Não importa o “tamanho” do número, você escreve combinando esses dez símbolos.
Nos sistemas egípcio e romano, sempre pode-se pensar a criação de novos símbolos para números que expressem quantidades maiores, precisam-se de números infinitos. Já no SND, o número finito de símbolos, apenas 10, possibilita escrever qualquer número.
Para calcular, a primeira máquina de contar foi a mão. Depois, a partir da correspondência um a um, as pedras substituem os dedos.
O monte de pedras, informa Ifrah (1997), deu origem à arte de calcular e o ábaco foi sempre utilizado, principalmente, antes da época em que não se conheciam os algarismos.
Aliás, a palavra cálculo vem do latim calculus que significa exatamente pedrinha.
O ábaco é uma evolução de montes de pedras. Enfileiravam-se colunas de pedras e ao tirar ou acrescentar pedras de um monte para outro, novas regras e possibilidades de cálculo foram sendo aperfeiçoadas.
Como instrumento mecânico de computação, de calcular, o ábaco pode ser visto como o mais antigo. Vários tipos de ábacos surgiram em diversos lugares dos mundos antigo e medieval.
Os sistemas de numeração escritos, antigos, como o egípcio e o romano, não eram muito propícios para efetuar operações aritméticas, para tal se usava o ábaco.
O sistema de numeração hindu tornou-se verdadeiramente efetivo e eficaz para cálculos e os hindus eram exímios calculadores.
Os árabes introduziram o sistema hindu-arábico na Europa. Fibonacci, no ano de 1202, completamente convicto de como esse sistema era superior publicou o Liber abaci influenciado pela obra de Al-Khowârizmi. (EVES, 2011).
Mas foram necessários séculos para que o sistema hindu-arábico se impusesse.
A história da Matemática narra as verdadeiras batalhas que travaram abacistas (os que defendiam os cálculos com ábaco) e os algoristas (aqueles que lutavam pela implantação do sistema hindu-arábico com os algoritmos).
Querendo Encontrar Formas de Que Seus Alunos Não Errem Mais as Contas
Faça uma Pedagogiação1.5.
Se você, professora, está lendo este texto, é porque já faz Pedagogiação. Porém, a sua ação pedagógica não está atingindo completamente seus objetivos.
Seus alunos continuam errando as contas, os algoritmos.
Isso porque a sua Pedagogiação, embora consciente e intencional, é inorgânica.
Você, professora, precisa transformar sua ação em sala de aula. Faça uma Pedagogiação1.5, uma ação pedagógica também consciente, intencional, porém, orgânica, porque cientificamente orientada.
Desperte a Cientista da Educação que está adormecida em você. Rememore, professora, Pedagogia é a Ciência da Educação, portanto você é uma Cientista da Educação.
A Pedagogiação1.5 é cientificamente orientada porque usa um Método Inovador, Único, Revolucionário: a Pedagogia1.5.
Nesse método, a Pedagogiação1.5 como ferramenta metodológica central, usa Vídeos-oficinas cuja estratégia de ensino utiliza História em quadrinhos, Fotografia, Pintura, Publicidade e Animação.
Experimente GRÁTIS o Minicurso Pedagogia1.5: são 4 vídeos-oficinas prontos para você, professora, usar em sala de aula para introduzir o Sistema de Numeração Decimal – SND.